光学薄膜特性理论计算2-传输矩阵法

发表于 分类于 ， 本文字数： 4.3k 阅读时长 ≈ 4 分钟

摘要

本文通过等效导纳的方法，推导出薄膜的特征矩阵并给出了数值计算方法。

1.单层介质薄膜

1.1 特征矩阵

单层薄膜的两个界面在数学上可以使用一个等效界面来表示，我们记等效后的导纳为组合导纳Y。

膜层等效

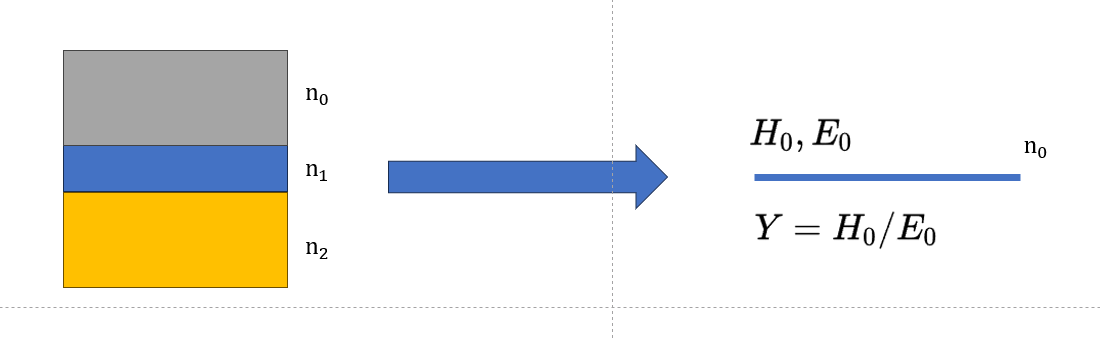
因此单层膜的反射系数可以表示为

\[ r = (\eta_0 - Y)/(\eta_0 + Y) \]

下面只需要计算有效导纳，将所有同方向的取相同符号，对于边界条件有

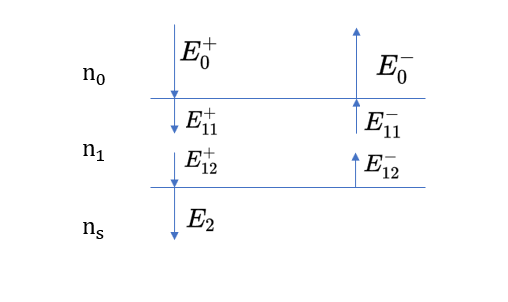
单层膜电场

\[ E_0 = E_0^+ + E_0^- = E_{11}^+ + E_{11}^- \]

\[ H_0 = H_0^+ +H_0^- = \eta_1 E_{11}^+ - \eta_1 E_{11}^- \]

在薄膜上传播的波会出现相位差，所以记

\[ E_0 = E_{12}^+ e^{-i\delta_1} +E_{12}^- e^{i\delta_1} \]

\[ H_0 = \eta_1 e^{-i \delta_1 } E_{12}^+ - \eta_1 e^{-i \delta_1 }E_{12}^- \]

用矩阵表示

\[ \begin{bmatrix} E_0\\ H_0 \end{bmatrix} = \begin{bmatrix} e^{- i \delta_1 } & e^{i \delta_1}\\ \eta_1 e^{-i \delta_1 } & - \eta_1 e^{i \delta_1 } \end{bmatrix} \begin{bmatrix} E_{12}^+\\ E_{12}^- \end{bmatrix} \]

同理在界面2处有

\[ E_2 = E_{12}^+ +E_{12}^- \]

\[ H_2 = \eta_1 E_{12}^+ - \eta_1 E_{12}^- \]

用矩阵表示

\[ \begin{bmatrix} E_{12}^+\\ E_{12}^- \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2 \eta_1} \\ \frac{1}{2} & - \frac{1}{2 \eta_1} \end{bmatrix}\begin{bmatrix} E_2\\ H_2 \end{bmatrix} \]

两式合并

\[ \begin{bmatrix} E_0\\ H_0 \end{bmatrix} = \begin{bmatrix} e^{-i \delta_1 } & e^{i \delta_1}\\ \eta_1 e^{-i \delta_1 } & - \eta_1 e^{i \delta_1 } \end{bmatrix} \begin{bmatrix} \frac{1}{2} & \frac{1}{2 \eta_1} \\ \frac{1}{2} & - \frac{1}{2 \eta_1} \end{bmatrix}=\begin{bmatrix} \cos{\delta_1} & -\frac{i}{\eta_1} \sin{\delta_1} \\ {-i\eta_1} \sin{\delta_1} & \cos{\delta_1} \end{bmatrix}\begin{bmatrix} E_2\\ H_2 \end{bmatrix} \]

等效导纳为\(Y = H_0/E_0\)，上式也可以写作

\[ E_0\begin{bmatrix} 1\\ Y \end{bmatrix} =\begin{bmatrix} \cos{\delta_1} & -\frac{i}{\eta_1} \sin{\delta_1} \\ {-i\eta_1} \sin{\delta_1} & \cos{\delta_1} \end{bmatrix}\begin{bmatrix} 1\\ \eta_2 \end{bmatrix}E_2 \]

矩阵\(\begin{bmatrix} \cos{\delta_1} & -\frac{i}{\eta_j} \sin{\delta_j} \\ {-i\eta_j} \sin{\delta_j} & \cos{\delta_j} \end{bmatrix}\)被定义为膜层的特征矩阵。

1.2 仿真代码

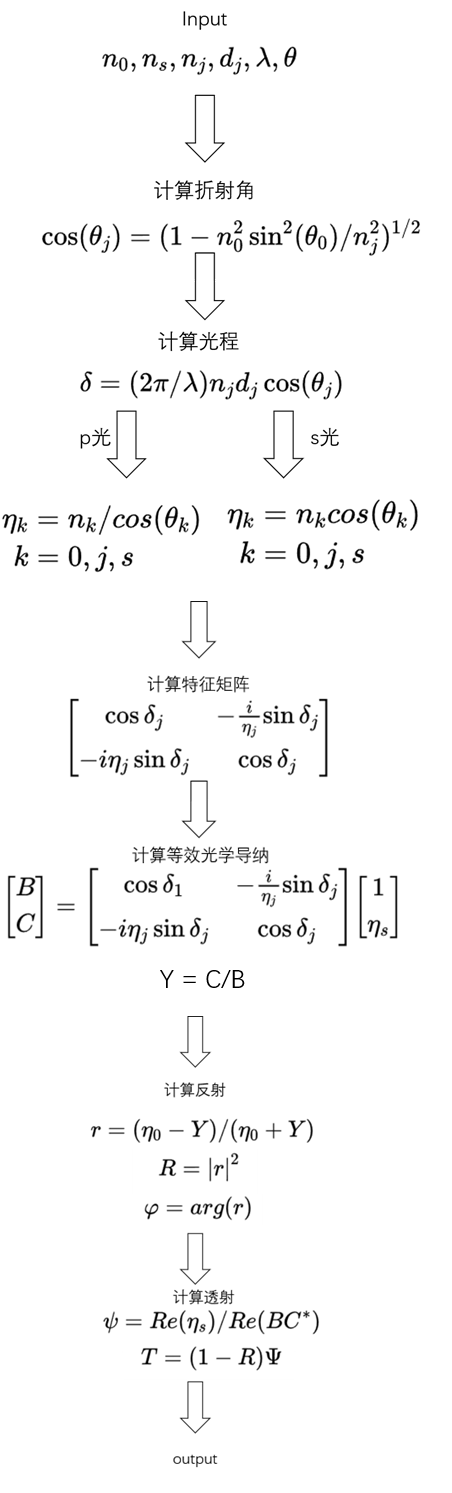
下面给出单层膜计算的流程图和matlab仿真代码，其中透反射与zemax仿真结果一致，

单层膜计算流程图 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
% 传输矩阵
function [Ms,Mp] = GET_single_TRM(n0,n,d,wavelength,theta0)
% 入射介质折射率 中间层折射率 中间层厚度 中间层折射率波长 入射角

costheta1 = sqrt(1-(n0^2*sin(theta0)^2)/(n^2));

deta = (2*pi/wavelength)*(n*d*costheta1);


eta_p1 = n/costheta1;
eta_s1 = n*costheta1;

% 计算s光传输矩阵
a1 = cos(deta);
a2 = -1i*sin(deta)/eta_s1;
a3 = -1i*sin(deta)*eta_s1;
a4 = cos(deta);
Ms = [a1,a2;a3,a4];

% 计算p光传输矩阵
a1 = cos(deta);
a2 = -1i*sin(deta)/eta_p1;
a3 = -1i*sin(deta)*eta_p1;
a4 = cos(deta);
Mp = [a1,a2;a3,a4];
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
clc
clear
close all
% 定义参数 单位微米
theta_ls = linspace(0, 90, 500);
wavelength = 0.55;
N_BK7 = 1.5214145;
N_air = 1;
N_my = 1.38;
N_AL = 0.7+ 7i;

n0 = N_air;
ns = N_air;
%d = wavelength/N_BK7*0.25;
d = 10;

% 申请空间
% theta_ls = 0;
Rs = zeros(size(theta_ls));
Rp = zeros(size(theta_ls));
Ts = zeros(size(theta_ls));
Tp = zeros(size(theta_ls));
S_phi_R = zeros(size(theta_ls));
P_phi_R = zeros(size(theta_ls));
S_phi_T = zeros(size(theta_ls));
P_phi_T = zeros(size(theta_ls));

for idx = 1:numel(theta_ls)
    theta0 = theta_ls(idx);
    theta0 = deg2rad(theta0);
    [Ms,Mp] = GET_single_TRM(N_air,N_BK7,d,wavelength,theta0);

    eta_p0 = n0/cos(theta0);
    eta_s0 = n0*cos(theta0);
    costhetas = sqrt(1-n0^2*sin(theta0)^2/(ns^2));
    eta_ps = ns/costhetas;
    eta_ss = ns*costhetas;
    
    % s光
    combMYs = Ms*[1;eta_ss];
    ys = combMYs(2)/combMYs(1);
    rs = (eta_s0 - ys)/(eta_s0 + ys);
    Rs(idx) = abs(rs)^2;
    % 势透射率
    Psi = real(eta_ss)/real((combMYs(1))*(conj(combMYs(2))));
    Ts(idx) = (1 - Rs(idx))*Psi;
    S_phi_R(idx) = angle(rs)/pi*180;
    % p光
    combMYp = Mp*[1;eta_ps];
    yp = combMYp(2)/combMYp(1);
    rp = (eta_p0 - yp)/(eta_p0 + yp);
    Rp(idx) = abs(rp)^2;
    Psi = real(eta_ps)/real((combMYp(1))*(conj(combMYp(2))));
    Tp(idx) = (1-Rp(idx))*Psi;
    P_phi_R(idx) = angle(rp)/pi*180;
end


figure;
plot(theta_ls, Rs);
hold on;
plot(theta_ls, Rp);
plot(theta_ls,(Rs+Rp)/2);
title('Reflectivity');

figure(2);
plot(theta_ls,Ts);
hold on;
plot(theta_ls,Tp);
plot(theta_ls,(Ts+Tp)/2);
title('transmission');

当把薄膜的有效光学厚度改为1/4波长的整数倍时候，如theta0 = 0;时、d = wavelength/N_BK7*0.25;在参考波长处传输矩阵会变成

1
2
3
4
5
6
7
8
9
Ms =

   0.0000 + 0.0000i   0.0000 - 0.6573i
   0.0000 - 1.5214i   0.0000 + 0.0000i

Mp =

   0.0000 + 0.0000i   0.0000 - 0.6573i
   0.0000 - 1.5214i   0.0000 + 0.0000i

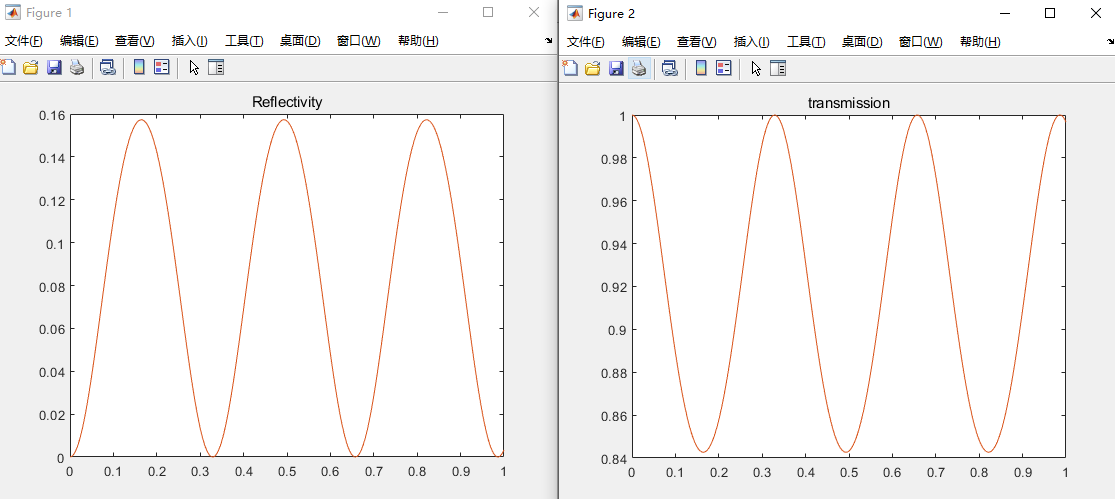
奇数倍时，特征矩阵的主对角线为0，此时膜系对透射和反射特性没有任何影响，被称为“虚设层”，而偶数倍时，会出现反射率的极值。厚度与反透射变化关系如下图，入射角为0度，横坐标单位为一个波长。

厚度和反透射关系

2.传输矩阵法

多层膜的计算方法和单层膜相似，使用特征矩阵方法计算，特征矩阵如下：

\[ \prod_{j=1}^{K} \begin{bmatrix} \cos{\delta_j} & -\frac{i}{\eta_j} \sin{\delta_j} \\ {-i\eta_j} \sin{\delta_j} & \cos{\delta_j} \end{bmatrix} \]

总体计算流程图如下

流程图

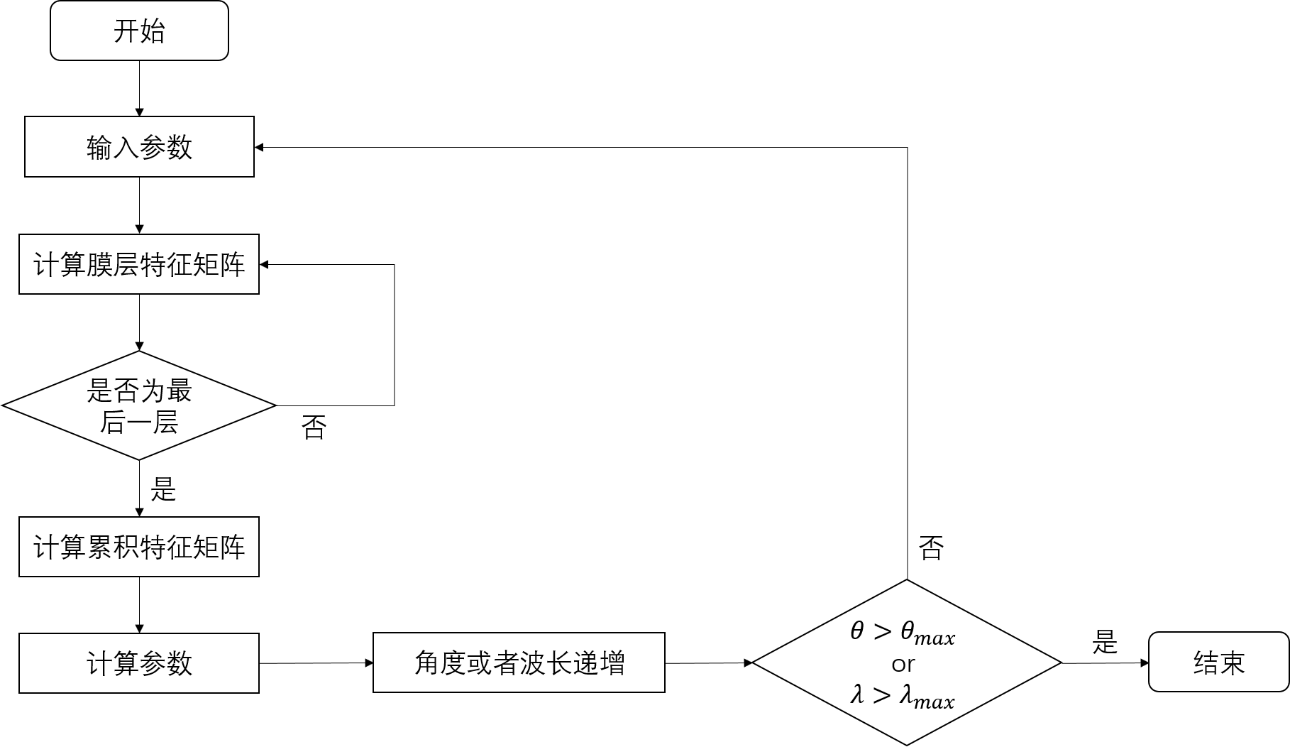
多层膜与单层类似，只需要多加一个循环即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
% 循环膜层
for idx2 = 1:numel(n_ls)
    nj = n_ls(idx2);
    dj = d_ls(idx2);            
    [Ms,Mp] = GET_single_TRM(n0,nj,dj,wavelength,theta0);
    if idx2 == 1
        Ms_all = Ms;
        Mp_all = Mp;
    else
        Ms_all = Ms_all * Ms;
        Mp_all = Mp_all * Mp;
    end
end

参考资料

[1] 唐晋发.现代光学薄膜技术.浙江大学出版社.2006年