加速度传感器校准方法分析

发表于 2023-11-16 分类于学习笔记，电子本文字数： 4.9k 阅读时长 ≈ 4 分钟

摘要

为防止俯仰角、四元数等概念干扰主题，这里以测xy平面角度的水平尺应用为例介绍加速度传感器的误差来源与校准方法，使用两个维度便于理解，扩展到多个维度同理可得。

加速度传感器原理

根据牛顿第二定律\(F=ma\)可知测量加速度等价于测量受力，在三维笛卡尔空间中，力又可以分解为三个坐标轴上的分量。因此在一个轴上，传感器可以简化等效为下图模型。

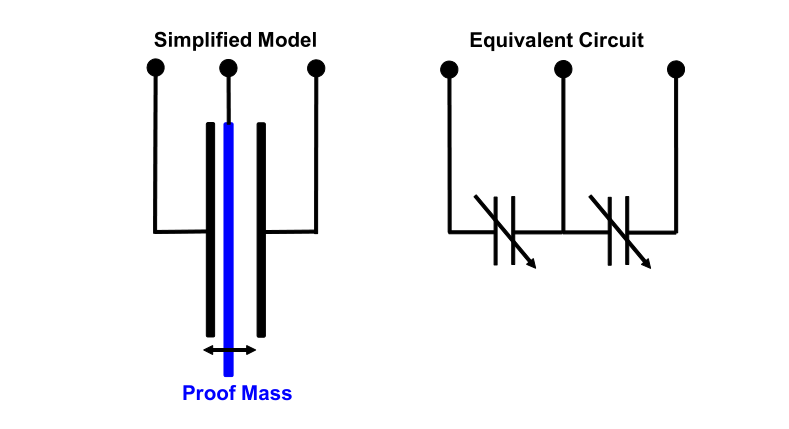
传感器芯片通过电容读取到加速度的大小并进行编码，总线上发出指令后它就会将测量到的数据传输出来。三轴应用最广泛的是在手机上，用于检测手机的朝向并进行屏幕的翻转。

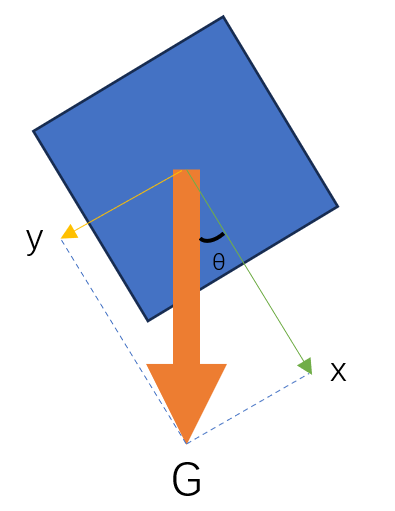
测量xy平面的角度需要两个轴，计算方法就是简单的三角函数\(\arctan(\frac{y}{x})\)，示意图如下。

误差分析

实际使用三角函数公式去处理传感器的返回值得到的角度肯定是不准确的，因为传感器的测量值本身存在误差。下面是几个典型的误差。

零点偏移

零点偏移是指在实际值为0g的时候传感器的输出值，示意图如下。

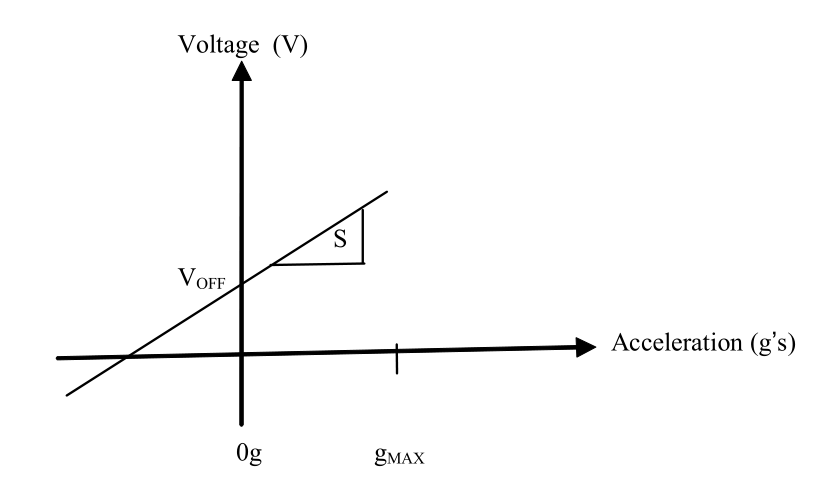
零点偏移产生的原因有很多种，比如出厂时Proof Mass并没有在中间的位置，温度也会影响零点位置。这里统一视作是零点偏移。这部分误差使用加减差值来处理。

尺度误差

这部分的误差来自于传感器的数字信号向物理量转换的误差，就和尺子一样，如果其刻度不均匀，量出的值也会不同。在测角度案例中通常体现为不同轴的数值不能等价。

这部分误差可以通过缩放来处理。

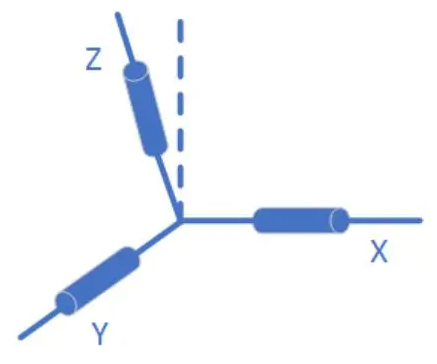
正交误差

传感器的三个轴不一定是完全正交的，这个很好理解就不多解释了。

机械误差

这部分误差是指传感器在贴片和组装为成品过程中产生的误差。

随机误差

白噪声和随机游走等干扰也会对测量产生误差，这类随机误差通常需要ALLAN方差校准来处理，也是比较难消除的一类误差。

校准方法

粗略校准法

在一个水平面上正向测出数据，如何旋转180°测得第二个值，在90°面上重复这一操作。可以获得4个数据，分别记为:

\[ [x_{max},y_{o1}], [x_{min},y_{o2}], [x_{o1},y_{max}], [x_{o2},y_{min}] \]

可以获得零偏和尺度，\(X_{offset} = \frac{x_{max}+x_{min}}{2}\),\(Y_{offset} = \frac{y_{max}+y_{min}}{2}\),\(S_{x} = \frac{x_{max}-x_{min}}{2}\),\(S_{y} = \frac{y_{max}-y_{min}}{2}\)

当然这是非常简单粗暴的做法。

六面校准法

结合上述的噪声(Bias and Noise)、尺度因子(Scale errors)和轴偏差(Axis misalignments)。建立加速度传感器的测量模型如下

\[ a^{B} = R T K (a^S + b + \nu) \]

其中\(a^{B}\)表示正交参考系坐标系下的加速度值，\(a^S\)表示传感器对应的非正交坐标系下的加速度值，R表示机械误差的旋转校正矩阵，T表示轴偏校正的变化矩阵，K表示尺度因子，\(b\)和\(\nu\)分别表示零偏和随机噪声。

以两个轴为例，a是一个\(2\times1\)的矩阵，RTK相乘视作一个\(2\times2\)的矩阵，忽略\(\nu\)，将\(b\)视作常数。可以得到如下方程

\[ \begin{bmatrix} A_x\\A_y \end{bmatrix}=\begin{bmatrix} a & b\\ c & d \end{bmatrix}\begin{bmatrix} A_{mx}\\A_{my} \end{bmatrix}+\begin{bmatrix} off_x\\off_y \end{bmatrix} \]

变为齐次方程坐标形式有

\[ \begin{bmatrix} A_{mx}&A_{my}&1 \end{bmatrix}\begin{bmatrix} a & c \\ b & d \\ off_x & off_y \end{bmatrix} = \begin{bmatrix} A_x & A_y \end{bmatrix} \]

使用最小二乘法求解上述方程，\(\beta = (X^T X)^{-1}X^T Y\)，其中\(\beta\)是参数矩阵，X是测量值，Y是理论值。理论值是将传感器按轴向位置放置测量。这里只给出了2个轴向的方程推导，3轴校准也是同理，参见参考资料^[2]

椭圆校准法

理想的xy轴数据在坐标系中的分布应当为圆形，但由于受到误差影响，实际会呈现出椭圆形状，如下图所示

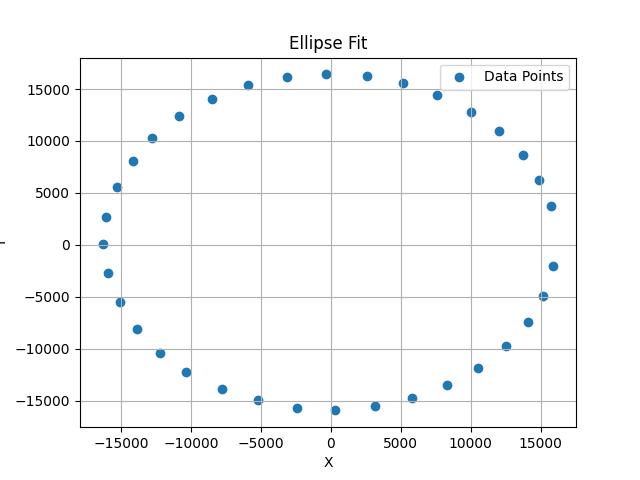
椭圆的方程为

\[ \left ( \frac{x-x_0}{A} \right )^2 + \left ( \frac{y-y0}{B} \right ) ^2 = 1 \]

其中\(x_0\)和\(y_0\)为椭圆中心的偏移值即零偏误差，\(A\)和\(B\)是椭圆的两个轴即尺度因子。所以通过最小二乘法拟合椭圆参数即可得到校准值。将上式展开有

\[ x^2+ay^2+cx+dy+f = 0 \]

其中\(a = \frac{A^2}{B^2},c = -2x_0,d=-2Y_0\frac{A^2}{B^2},f = x_0^2 + \frac{A^2}{B^2}y_0^2 - A^2\)

取误差函数为

\[ e_i(a,c,d,f) = x_i^2+ay_i^2+cx_i+dy_i+f \]

则误差的平方和为

\[ E_i = \sum_{i=1}^{N} e_i^2 \]

要求对\(a,c,d,f\)的一阶偏导为零，可得方程组

\[ \left\{\begin{matrix} \frac{\partial E}{\partial a}=0\\ \frac{\partial E}{\partial c}=0\\ \frac{\partial E}{\partial d}=0\\ \frac{\partial E}{\partial f}=0 \end{matrix}\right. \Longrightarrow \left\{\begin{matrix} \sum_{i=1}^{N} e_i y_i^2 = 0\\ \sum_{i=1}^{N} e_i x_i = 0\\ \sum_{i=1}^{N} e_i y_i = 0\\ \sum_{i=1}^{N} e_i = 0 \end{matrix}\right. \]

使用\(\bar{x}\)代替平均值\(\frac{1}{N}\sum_{i=1}^{N}x_i\)的记法，将上式展开，有

\[ \left\{\begin{matrix} \overline{x^2y^2} + a \overline{y^4} + c\overline{xy^2} + d \overline{y^3} + f \overline{y^2} = 0 \\ \overline{x^3} + a \overline{x y^2} + c\overline{x^2} + d \overline{xy} + f \overline{x} = 0\\ \overline{x^2y} + a \overline{y^3} + c\overline{xy} + d \overline{y^2} + f \overline{y} = 0 \\ \overline{x^2} + a \overline{y} + c\overline{x} + d \overline{y} + f = 0 \end{matrix}\right. \]

写成矩阵形式有

\[ \begin{bmatrix} \overline{y^4} & \overline{xy^2} & \overline{y^3} & \overline{y^2}\\ \overline{x y^2} & \overline{x^2} & \overline{xy} & \overline{x}\\ \overline{y^3} & \overline{xy} & \overline{y^2} & \overline{y}\\ \overline{y} & \overline{x} & \overline{y} & 1 \end{bmatrix}\begin{bmatrix} a\\ c\\ d\\ f \end{bmatrix} = \begin{bmatrix} -\overline{x^2y^2}\\ -\overline{x^3}\\ -\overline{x^2y} \\ -\overline{x^2} \end{bmatrix} \]

求解方程即可计算出几个参数的值，使用python进行数据计算

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

data = pd.read_csv("data.csv")
x = np.array(data.loc[:, "x"])
y = np.array(data.loc[:, "y"])


num_points = len(x)
# 绘制数据点
plt.scatter(x, y, label='Data Points')

# 一次统计平均
x_var = sum(x)/num_points
y_var = sum(y)/num_points
# 二次统计平均
xx_var = sum(x**2)/num_points
yy_var = sum(y**2)/num_points
xy_var = sum(x*y)/num_points
# 三次统计平均
xxx_var = sum(x*x*x)/num_points
yyy_var = sum(y*y*y)/num_points
xxy_var = sum(x*x*y)/num_points
xyy_var = sum(x*y*y)/num_points
# 四次统计平均
xxxx_var = sum(x*x*x*x)/num_points
yyyy_var = sum(y*y*y*y)/num_points
xxyy_var = sum(x*x*y*y)/num_points


A0 = np.array([[yyyy_var,xyy_var,yyy_var,yy_var],
              [xyy_var,xx_var,xy_var,x_var],
              [yyy_var,xy_var,yy_var,y_var],
              [yy_var,x_var,y_var,1]])

b = np.array([-xxyy_var,-xxx_var,-xxy_var,-xx_var]).T

A1 = np.linalg.inv(A0)
resoult = np.dot(A1,b)

x0 = -resoult[1]/2
y0 = -resoult[2]/(2*resoult[0])
AA = np.sqrt(x0*x0 + resoult[0]*y0*y0 - resoult[3])
BB = AA/np.sqrt(resoult[0])

print(x0,y0,AA,BB)
# 生成角度值
theta = np.linspace(0, 2 * np.pi, 100)

# 计算椭圆上的点坐标
x_fit = x0 + AA * np.cos(theta)
y_fit = y0 + BB * np.sin(theta)
plt.plot(x_fit, y_fit, color = 'r',label='fit ellipse')

plt.legend()
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Ellipse Fit')
plt.grid(True)
plt.show()

拟合结果如下：

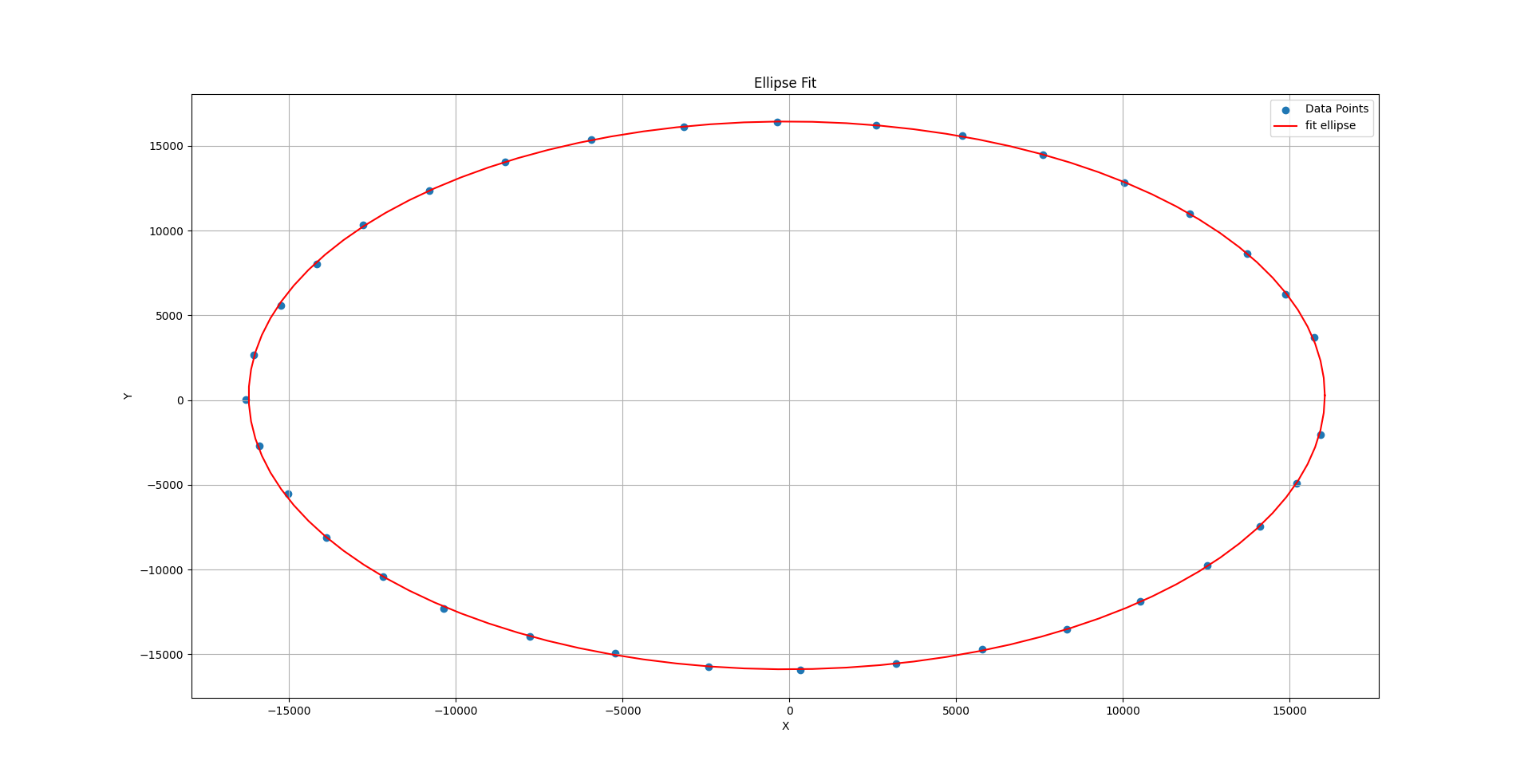
椭球校准推导和matlab代码见参考资料^[3]