信号与系统(1)--信号与系统
摘要
信号与系统是电子信息类的专业基础课程,本系列将奥本海姆的《信号与系统》一书,系统地复习该课程。本篇将介绍什么是信号,什么是系统。
1.信号
1.1 什么是信号?
我们的大脑无时无刻不在处理神经元传来的电信号,计算机每一秒都在处理数以亿记的01信号。其中的信号是什么?它们是如何被处理的?在数学上,信号可以表示为一个或多个变量的函数,比如我们接收到了一个语音信号波形如下。
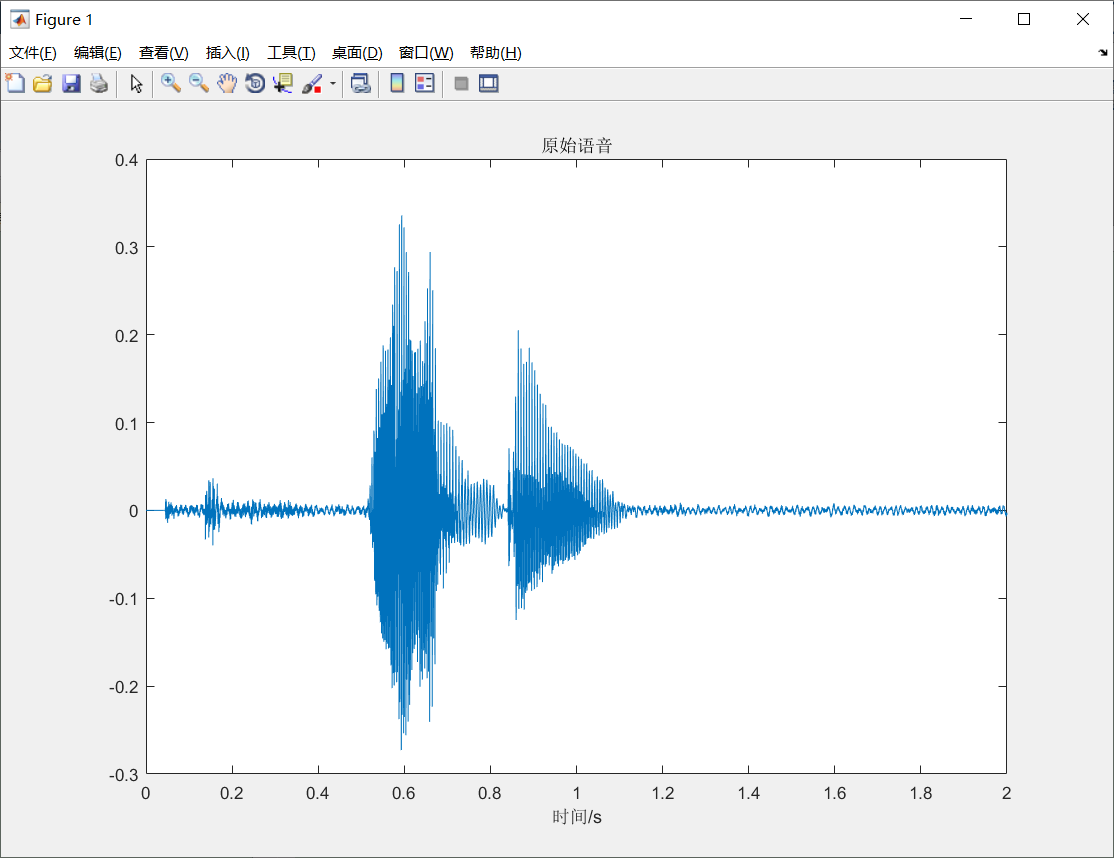
这是一句“亮灯”的语音信号波形。这类自变量和应变量都是连续的信号被称为连续信号,相反如果一个信号的自变量或应变量是离散值,我们记其为离散信号,二者差异可见下图。
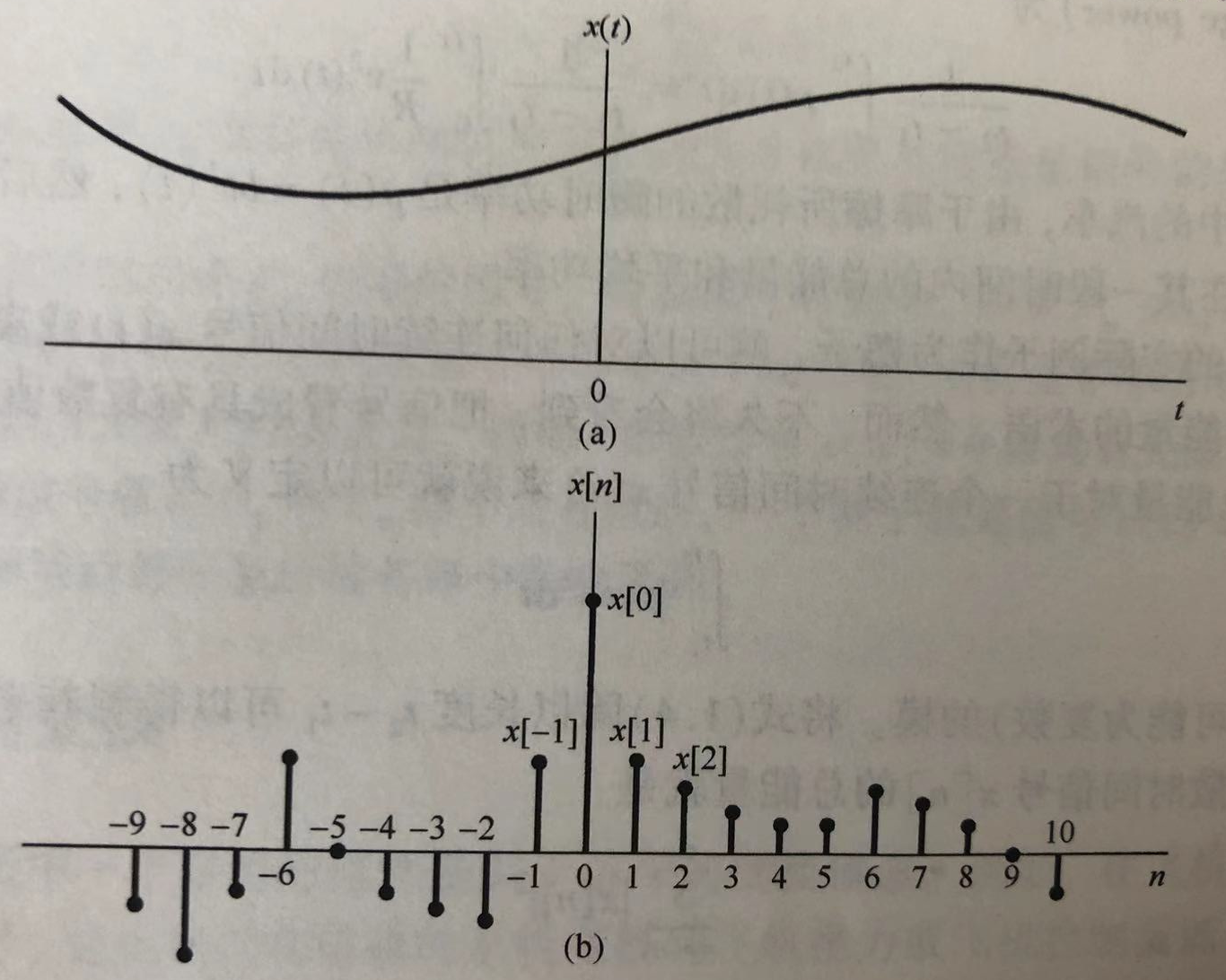
为了区分连续信号和离散信号,我们做出如下约定自变量如果是连续时间,我们记为t,信号函数记为\(x(t)\)。如果是离散时间则记为n,信号函数记为\(x[n]\)。
1.2 信号的变换
借助数学形式,我们可以将很多时间为自变量的信号都函数化,这样一些函数的性质也可以作用于信号上。一种非常简单但同时很重要的变化例子就是时移(time shift)。在不同位置的接收机收到发射机的信号会因距离不等而造成传播时间上的差别,这就可以使用时移变化来描述。
第二种典型的自变量变化就是时间反转(time reversal),常见的处理过程就是倒放,另一种处理方法是倍速,对应了时间尺度变化(time scaling)。
综合上述几种变化,对应到数学函数上无非就是\(x(t)\)-->\(x(\alpha t + \beta)\)。这里变化并不复杂,就不给出具体实例了,需要熟练掌握的可以翻看任意教材的信号变化部分习题。
1.3 奇偶与周期
函数具有奇偶性,如果一个信号以原点为轴反转后不变,就称其为偶(even)信号。 \[ x(-t) = x(t) \] 如果是 \[ x(-t)=-x(t) \] 则称其为奇(odd)信号。
一个重要的事实是,任何信号都可以看作是一个奇信号和一个偶信号的和。 \[ \begin{align} Ev\left \{ x(t) \right \} = \frac{1}{2}[x(t)+x(-t)] \nonumber \\ Od\left \{ x(t) \right \} = \frac{1}{2}[x(t)-x(-t)]\nonumber \end{align} \]
周期(periodic)信号也是一种非常常见的信号,对于一个周期连续时间信号有:
\[ x(t) = x(t+T) \]
其周期为T。如果对于任意的t和任意的整数m都有\(x(t)=x(t+mT)\)则使式成立的最小正值T称为\(x(t)\)的基波周期(fundamental period)。
1.4 三角函数与指数
正弦信号(sinusoidal signal)是一种非常典型的信号,其数学表达式为: \[ x(t)=A\cos{(\omega_0 t + \phi)} \]
其中通常使用秒作为t的单位,则\(\phi\)的单位为弧度(rad),\(\omega_0\)的单位就是rad/s。
根据欧拉公式,正弦信号可以用复指数信号(complex exponential signal)来表示
\[ A \cos{(\omega_0 t + \phi)}=\frac{A}{2}e^{j\phi}e^{j\omega_0t} + \frac{A}{2}e^{-j\phi}e^{-j\omega_0t} \]
\[ \begin{aligned} A\cos(\omega_0t+\phi) & = ARe\{ e^{j(\omega_0t+\phi)}\} \\ A\sin(\omega_0t+\phi) & = AIm\{ e^{j(\omega_0t+\phi)}\} \end{aligned} \] 其中\(Re\)和\(Im\)分别是取实部和取虚部。
1.5 能量与功率
数学函数可以表示信号,但信号只有结合物理才有实际意义,电信号是常见的信号,例如,设\(v(t)\)和\(i(t)\)分别是阻值为R的电阻上的电压和电流信号,那么其瞬时功率就是:
\[ p(t)=v(t)i(t)=\frac{1}{R}v^2(t) \]
在时间\([t_1,t_2]\)间消耗的总能量为\(\int_{t_1}^{t_2}p(t)dt\),其平均功率(average power)为:
\[ \frac{1}{t_2-t_1}\int_{t_1}^{t_2}p(t)dt = \frac{1}{t_2-t_1}\int_{t_1}^{t_2}\frac{1}{R}v^2(t)dt \]
根据平均功率,我们可以将信号分为三类:
- 有限能量信号(\(E_\infty < \infty\)),这类信号的平均功率必须为0,否则积分后能量就会变成无穷大
- 有限功率信号(\(P_\infty < \infty\)),这类信号能量是无穷大的,但平均功率不是。
- 无限功率信号,一个典型的例子是\(x(t) = t\)
1.6 单位阶跃与单位脉冲
连续时间的单位阶跃函数\(u(t)\)的定义是
\[ u(t) = \left \{ \begin{matrix} 0, t < 0\\ 1, t>0 \end{matrix}\right. \]
单位阶跃再\(t=0\)点处是不连续的,对其取一次微分就得到了冲激函数\(\delta(t)\),这个函数在数学中是不存在的,但是在物理学中它很好用于是就被拿来用了。在工学中这个函数也是极具理论价值,但为了能实际应用,冲激函数被近似认为是非常短的时间间隔\(\Delta\)内完成的从0到1的阶跃函数的微分。
离散时间的单位脉冲和单位阶跃序列也是同理,积分和微分分别对应求和和差分。
2.系统
2.1 什么是系统?
在实际过程中信号仅仅是作为输入或者输出的一部分内容,信号是如何被处理的还得通过系统。通常使用如下的方式来表示连续时间的输入输出关系:
\[ x(t) \to y(t) \]
同理,离散的表示符号为:
\[ x[n] \to y[n] \]
还是以电路作为例子,下面是一个简单的RC电路:
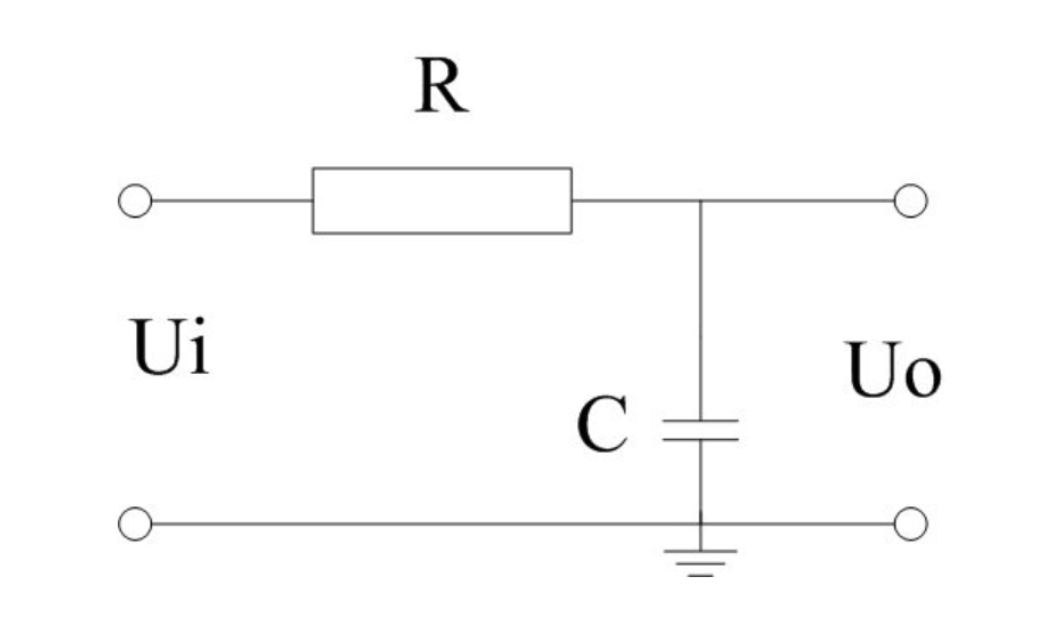
这可以看作是一个简单的系统,其中输入电压是\(u_i(t)\),输出信号是\(u_o(t)\),根据欧姆定律有,流经电阻的电流\(i(t)\)应当正比于电阻上的电压。
\[ i(t) = \frac{u_i(t)-u_o(t)}{R} \]
同时电流还可以通过电容器上的电压变化率计算得到:
\[ i(t) = C\frac{du_o(t)}{dt} \]
联立两式即可得到输入输出的微分关系方程
\[ \frac{du_o(t)}{dt} +\frac{1}{RC}u_o(t) = \frac{1}{RC} v_i(t) \]
这是一个非常常见的系统,同时也是一个简单的一阶线性微分方程,这样一来系统也数学化了,系统代表了一个方程或者等式。
2.2 系统的互联
很多实践中的系统其实都是非常简单的系统组合而成,常见的组合方法有串联(series interconnection)或级联(cascade interconnection)、并联(parallel interconnection)、反馈互联(feedback interconnection)。
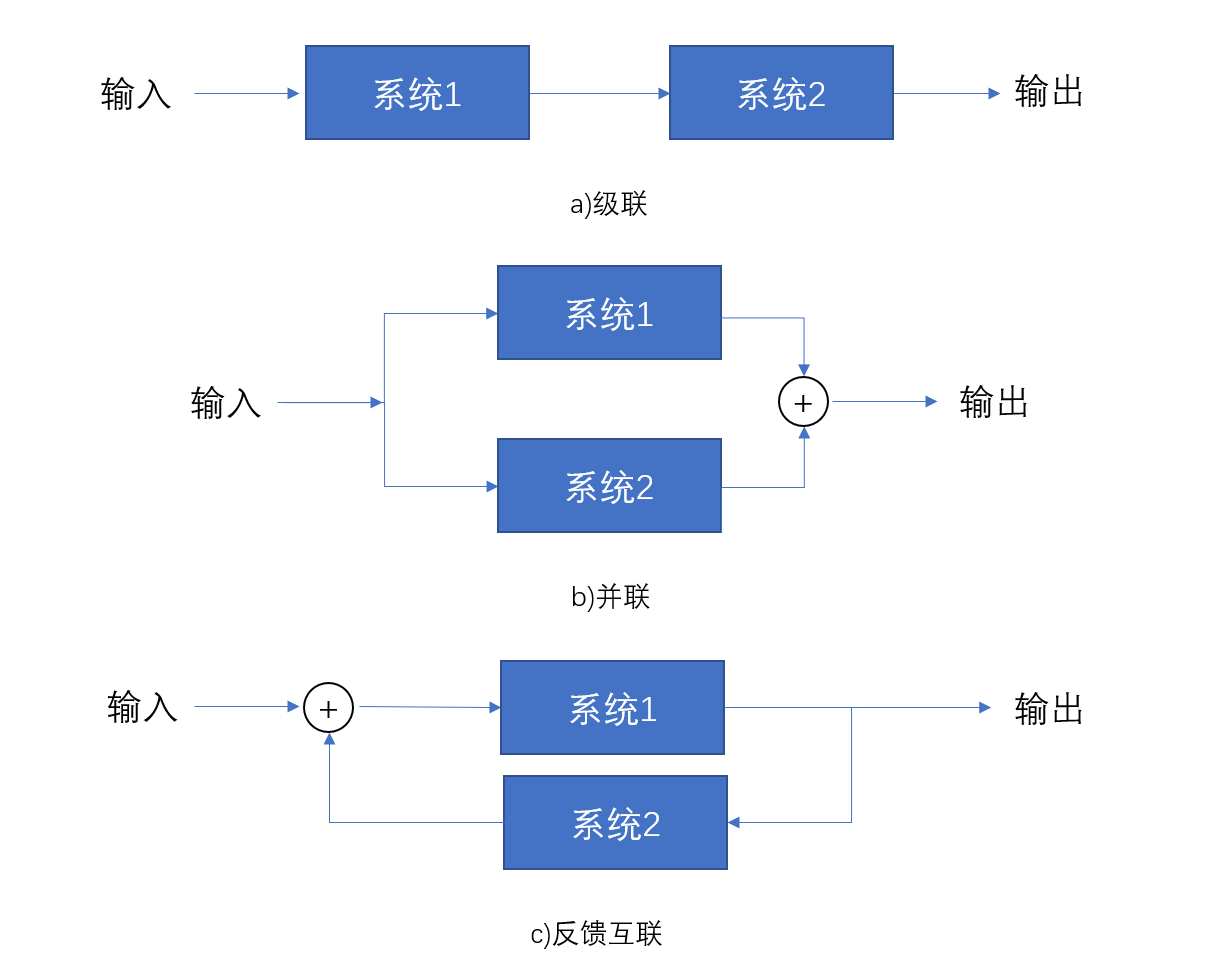
虽然图像表示得已经很清楚了,这里还是需要补充一些。
级联通常发生在对信号连续处理的过程,比如收音机收到信号后进行解调后通过放大器放大信号。反馈也是一个重要的系统类型,比如在定速巡航中,汽车会通过监控车速来控制能量的传递,而车速快慢是由发动机提供的能量决定的。
最后这三种互联方式也可以进行彼此间组合形成更复杂的系统。
2.3 系统的性质
2.3.1 记忆性
如果系统的输出仅仅取决于该时刻的输入,该系统就被称为无记忆(memoryless)系统,一个简单的例子就是恒等系统(identitiy system),该系统的输出就等于输入。
一个典型的有记忆系统就是积分器,或者对应离散信号的累加器(accumulator)。在实际中,使用储能元件,如电容,就可以实现这一系统。又记忆系统不仅包括存储过去信息,存储将来信息也算是有记忆系统。
2.3.2 可逆性
一个系统如果在不同输入下会产生不同输出,该系统就是可逆的(invertible),它就会有一个对应逆系统(inverse system),当原系统和逆系统进行级联后,输入就会等于输出,系统就变成了一个恒等系统。
不可逆系统的不同输入可能会对应同一种输出,比如说\(y(t)=x^2(t)\)。
2.3.3 因果性
如果一个系统在任何时刻的输出只取决于现在的输入和过去的输入,该系统就被称为因果(causal)系统。因果系统是无法根据输出预测未来的输入值的,且对于一个因果系统两个输入直到某一时间都是相同的,那其输出必然相同。
时间相关的现实系统几乎都是因果的,但对于一些数据处理系统,它并不局限于因果,比如图像处理中的窗口平滑系统。
2.3.4 稳定性
稳定性(stability)是指系统在很小的输入下响应不会发散。如单摆、RC电路中,能量会逐渐消耗并趋向于稳定。而对于不稳定系统,其输出会不断增加,想要判别系统是不稳定系统就学要找出一个特定的有界的输入使得输出无界。
2.3.5 线性
线性系统的一个重要特征就是叠加性质(superposition property),叠加性说的是:如果系统的输入是几个信号的加权和组成,那么输出信号也是每一个输入信号通过系统后的输出加权和。
用公式表示,简记小写字母为输入,大写字母为系统的对应输出,系统为函数f,输入为a时输出为\(A=f(a)\)。
对于系统有,当\(a=b+c+d\)时,\(A=f(b)+f(c)+f(d)=B+C+D\)。这被称为可加性(additivity)。还是这个系统,\(k_1\)是一个常数,当输入\(k_1a\)时,输出\(A=k_1f(a)\)。这被称为齐次性(homogeneity)
2.3.6 时不变性
通俗来说,只要系统的特性和行为不随时间改变,这个系统就是时不变的。今天研发出的系统到了明天性质就变了,那我们就失去了研发的意义,因此时不变性也是非常重要的一个性质。在实际生活中线性时不变系统是最为常用的一种系统。