统计学习(6)--逻辑斯谛回归
摘要
逻辑斯谛回归模型利用了逻辑斯谛方程的对数特性,将特征参数映射到[0,1]之间,将问题转换为概率预测,从而实现判别。
1.逻辑斯谛方程
学过数学建模的应该都知道,逻辑斯谛方程最早提出是用于人口增长模型。下面进行一个简单的推导。
假设人口随时间的函数是\(W(t)\),人口增长率为\(\beta\),则人口增长的微分方程为
\[ \frac{\mathrm{d} W(t)}{\mathrm{d} t} = \beta W(t) \]
解得
\[ W(t) = \exp (\beta t + C) \]
这种指数爆炸型增长是不太可能发生的,毕竟资源是有限的,所以人口增长应该还要和生物容量\(K\)有关,再重新写出微分方程,这里的\(\beta\)和上面的可能存在数值上的差异。
\[ \frac{\mathrm{d} W(t)}{\mathrm{d} t} = \beta W(t) (K-W(t)) \]
这就是逻辑斯谛方程的微分形式,其实这个方程虽然是推猜出来的,但其蕴含了一定的自然规律,所以他从人口模型应用到了其他各个领域,这点和傅里叶变换不谋而合。
2.逻辑斯谛分布
现在我不关心数量了,我更想知道现在的人口占总容量的多少,记比例为\(P(t)\)我们有\(P(t)=W(t)/K\)
对于P(t)有
\[ \begin{align} \frac{\mathrm{d} P(t)}{\mathrm{d} t} &= \frac{\mathrm{d} (W(t)/K)}{\mathrm{d} t} \\ &= \frac{\beta}{K}W(t)(K-W(t)) \\ &= K\beta P(t)[1-P(t)] \end{align} \]
等式就变成了微分方程 \[ \frac{1}{P[1-P]} P \mathrm{d} P = C * \mathrm{d} t \] 其中C是常数
解方程得
\[ P = \frac{\exp{(\alpha+\beta t)}}{1+\exp{(\alpha+\beta t)}}\tag{式1} \]
其中\(\alpha\)和\(\beta\)是常数,令\(x = \alpha+\beta t\)
将上式函数绘制出来就如下图
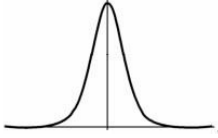
P的物理意义是占比,也就是说它的取值范围在\([0-1]\)之间,这和概率不谋而合,将这个函数视作概率密度函数,可以得到逻辑斯谛分布函数方程和图如下
\[ F(x)=P(X \leqslant x)=\frac{1}{1+\mathrm{e}^{-(x-\mu) / \gamma}} \]
\[ f(x)=F^{\prime}(x)=\frac{\mathrm{e}^{-(x-\mu) / \gamma}}{\gamma\left(1+\mathrm{e}^{-(x-\mu) / \gamma}\right)^{2}} \]
其中\(\mu\)为位置参数,\(\gamma>0\)是形状参数。

3.二项逻辑斯谛回归模型
对于二分类问题,使用统计学习中常用的\(w\)和\(b\)来代替式1的\(\beta\)和\(\alpha\),可以得到
\[ P = \frac{\exp (w \cdot x+b)}{1+\exp (w \cdot x+b)} \]
我们人为假定这个P是实例x在参数\(w\)和\(b\)条件下分类为1的概率,毕竟参数是可以训练的,那么有
\[ P(Y=0 \mid x)=\frac{1}{1+\exp (w \cdot x+b)} \]
两者的和为1,使用训练集训练数据后,对于新实例,只需要计算两者的概率让后进行归类即可。
模型的参数可以使用极大似然估计法来得到,设
\[ P(Y=1 \mid x)=\pi(x), \quad P(Y=0 \mid x)=1-\pi(x) \]
似然函数为
\[ \prod_{i=1}^{N}\left[\pi\left(x_{i}\right)\right]^{y_{i}}\left[1-\pi\left(x_{i}\right)\right]^{1-y_{i}} \]
对数似然函数为
\[ \begin{aligned} L(w) & =\sum_{i=1}^{N}\left[y_{i} \log \pi\left(x_{i}\right)+\left(1-y_{i}\right) \log \left(1-\pi\left(x_{i}\right)\right)\right] \\ & =\sum_{i=1}^{N}\left[y_{i} \log \frac{\pi\left(x_{i}\right)}{1-\pi\left(x_{i}\right)}+\log \left(1-\pi\left(x_{i}\right)\right)\right] \\ & =\sum_{i=1}^{N}\left[y_{i}\left(w \cdot x_{i}\right)-\log \left(1+\exp \left(w \cdot x_{i}\right)\right]\right. \end{aligned} \]
对\(L(w)\)用梯度下降法求极大值即可得到估计值。
最后给出多项逻辑斯谛回归的公式
\[ P(Y=k \mid x)=\frac{\exp \left(w_{k} \cdot x\right)}{1+\sum_{k=1}^{K-1} \exp \left(w_{k} \cdot x\right)}, \quad k=1,2, \cdots, K-1 \]
参考资料
[1] 《统计学习方法》 李航