统计学习(5)--决策树

发表于 2022-12-18 更新于 2023-01-07 分类于学习笔记，计算机本文字数： 4.1k 阅读时长 ≈ 4 分钟

摘要

决策树是一种基本的分类和回归方法，其具有可读性好，分类快等优点。在西瓜书中，决策树就作为例子引入了机器学习，说明了树模型是适合于新手入门学习的内容。本文会从基本概念逐一展开介绍几种决策树的基本算法。

1.什么是决策树

分类决策树是一种描述对实例进行分类的树形结构，正如书中西瓜好不好的决策判别。

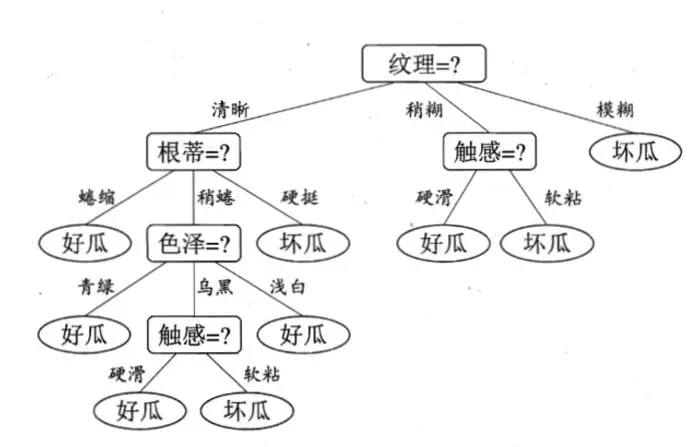
人可以同个经验来判别好坏瓜的条件，那对于机器来说，要如何实现并构造决策树呢？不可避免的我们需要一个判别依据，好在信息论里能够给我们一些启发。

2.信息熵

信息熵是用来衡量一个体系的不确定度的物理量，熵这个词也是借用的热力学，信息熵越大，不确定性越强。计算公式如下

\[ H(X)=-\sum_{i=1}^{M} P\left(x_{i}\right) \log _{2} P\left(x_{i}\right) \tag{1.1} \]

如果不太清楚这个概念可以通过该链接去了解一下信息量和信息熵

在理解信息熵这个概念后，这里再补充一个条件熵，它指的是在某一条件Y下体系具有的信息熵。公式如下

\[ H(X \mid Y)=-\sum_{i=1}^{M} P(x_i \mid Y) \log _{2} P(x_i \mid Y) \tag{1.2} \]

显然系统的条件熵要比信息熵要小一些，因为条件Y的发生让系统更加确定了一些，它们差值不妨就叫做信息增益。公式如下

\[ I(X, Y)=H(X)-H(X \mid Y)\tag{1.3} \]

2.判别条件

有了以上几个量化概念，我们就可以用来量化决策树。

可以看一个具体的例子，有一副去掉大小王的扑克牌(52张)，我从中随机抽取一张，想让机器狗旺财来帮我判别它是红色还是黑色。旺财无法直接识别颜色，它只能看见点数和花色,所以它需要用决策树的方法来处理这个问题。

旺财计算了一下该问题的信息熵

\[ \begin{align} H(X) & = -\sum_{i=1}^{M} P\left(x_{i}\right) \log _{2} P\left(x_{i}\right)\nonumber\\ & = \frac{1}{2} + \frac{1}{2} \nonumber \\ & = 1 \nonumber \end{align} \]

2.1 使用点数决策 \(Y_1\)

它决定先试试点数，决策条件为点数大于等于10的都是红色。

那么条件熵为

\[ H(X \mid Y_1) = (\frac{4}{13}+\frac{9}{13})\cdot (\frac{1}{4}\log_{2}{4}-\frac{3}{4}\log_{2}\frac{3}{4}) \approx 0.811 \]

好像这个条件并没有起到任何帮助，信息增益为\(I(X, Y_1)=0.189\)

2.2 使用花色决策 \(Y_2\)

旺财改变了策略，红桃的牌都是红色。

红桃牌的概率是1/4且全是红色那么条件熵为

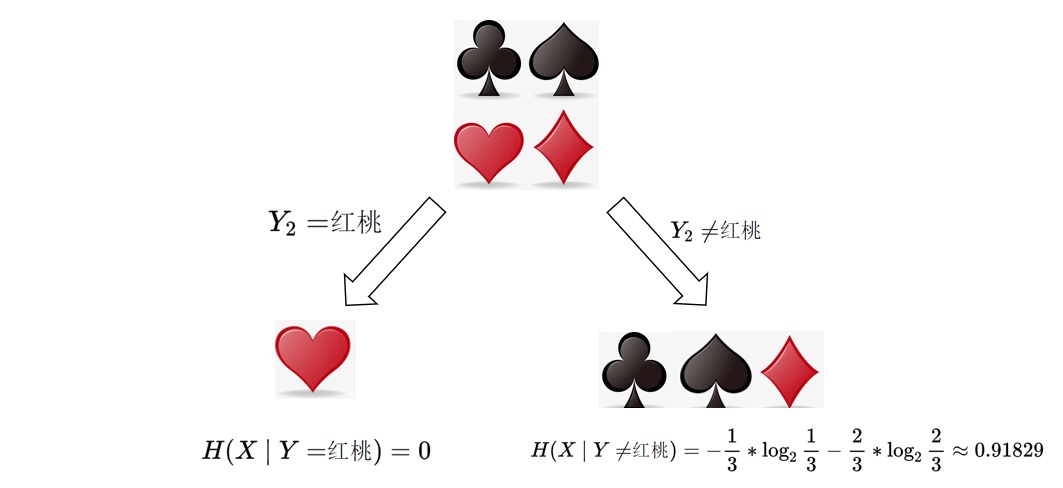
\[ H(X \mid Y_2) = \frac{1}{4} \cdot 0 + \frac{3}{4} \cdot 0.91829 \approx 0.689 \]

信息增益为\(I(X, Y_2)=0.311\)，看起来好了一些。

2.3 花色决策2.0 \(Y_3\)

旺财注意到上述决策中左节点的信息熵已经是0了，可以停止优化，而右节点的信息熵接近父节点的信息熵，说明优化空间很大，于是它对右节点再采策略认为方片也是红的。

毫无疑问信息信息增益达到了最大，旺财完美地完成了任务。

3.ID3算法

ID 是 Iterative Dichotomiser的缩写，迭代二分器/二叉树，虽然决策树不一定是二叉树，但通常情况下是二分的，3大概是第三代的意思吧。

上述这种以信息增益作为特征选择的度量，使用自顶向下的贪心算法遍历决策树空间的算法即为ID3算法。

通俗的讲该算法就是每一步都选择可以实现信息增益最大的特征作为该节点的分类条件直到特征用完或者分类结束。

程序流程图就放在后面给，现在来看看ID3算法优缺点。

3.1 ID3的优点

简单，只需要算信息熵就完了。
鲁棒性强，不容易受到噪声的影响
搜索空间完整，基本上会遍历所有特征

3.2 ID3的缺点

ID3算法会去选择可取值类别多的特征，这是信息熵的计算方法导致的，分得越细，确定性就会越高。
只能计算离散值
无法处理信息缺失
容易过拟合，因为它会遍历所有特征

4.C4.5算法

ID3 算法的发明人Ross Quinlan也意识到了这些缺点，有问题就解决呗，ID3会对多分类有个偏好，这是因为信息增益的计算方式导致的，为了解决这一问题，必须将判别条件改变。

为此分裂信息的定义被提出，计算公式如下：

\[ SplitInfo_A(D)=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \log _{2} \frac{\left|D_{i}\right|}{|D|}\tag{4.1} \]

其中D是数据集，\(D_i\)是D在特征A下的第i个分类子集。可以看出分裂信息也特征的类别越多值就会越大。

所以只要将信息增益除以分裂信息就可以得到一个消除倾向的判别条件，我们称为信息增益率，计算公式如下：

\[ \operatorname{GainRatio}(D,A)=\frac{I(D, A)}{\operatorname{SplitInfo_A}(D)} \tag{4.2} \]

对于连续的特征值，可以选择遍历这些值找到信息增益最大的分界点来实现对值的二分离散化。

信息缺失可以选择补上期望值，过拟合就采用剪枝的方法来完成。

这样问题就解决了不少，但这类算法还是存在硬伤。一是算法只能用于分类，二是构造过程需要反复遍历，比较大小，还是对数运算，算法效率低。

5.CART3算法

5.1 不如换个判别条件

既然对数运算费时，不如直接抛开熵这个数值条件，重新找一个判别依据，公式如下

\[ \operatorname{Gini}(D)=\sum_{k=1}^{K} \frac{\left|C_{k}\right|}{|D|}\left(1-\frac{\left|C_{k}\right|}{|D|}\right)=1-\sum_{k=1}^{K} p_{k}^{2} \tag{5.1} \]

我们称它为基尼系数，其中k为类别，\(p_k\)是k类别的概率，它可以识别当前集合的纯度。来看一个具体例子，当k只能取两个值时，如红色牌的概率为\(p_1\) 黑色牌概率为\(p_2\)，而且有\(p_1=1-p_2\)，代入式(5.1)可得基尼系数是一个关于\(p_1\)的二次函数，关系如下图

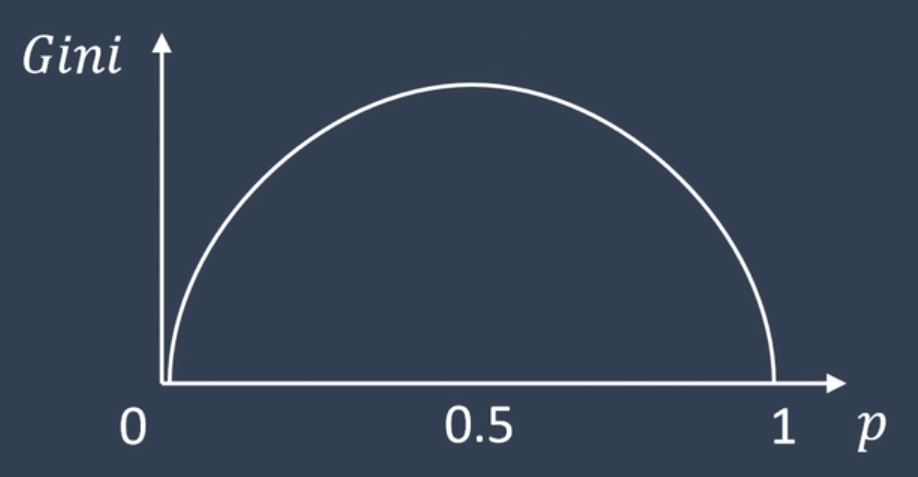
当集合中只有红色时，即概率\(p=1\)，这时基尼系数为0，当红黑参半时，基尼系数会达到最大。由此可见，基尼系数越小，代表集合纯度越高。

我们可以以此为参考依据，遍历特征，选出加权基尼系数最小的分类方法作为策略。同时CART3永远对数据二分，离散连续一视同仁，二叉树的便捷性也是显而易见的。

5.2 谁说树只能分类

CART树全名是Classification and Regression Tree，这说明它既能分类也能回归，回归树的构建本质上是用平方误差最小化准则进行特征选择，去生成二叉树。

其判别的条件又不是基尼系数了，而是最小均方差值，公式如下

\[ \min_{j, s}\left[\min_{c_{1}} \sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min_{c_2} \sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-c_{2}\right)^{2}\right] \tag{5.2} \]

其中因为特征是连续值，该公式的意思是选择第j个特征的s为切分点，这样集合就分为了\(R_1\)和\(R_2\)，使得两个区域的label值和该划分区域的值c平方和最小。得到j和s作为划分的依据，其中\(c_1\)、\(c_2\)取集合的均值： \[ c_{1}=\frac{1}{N_{1}} \sum_{x_{i} \in R_{1}} y_{i}, \quad c_{2}=\frac{1}{N_{2}} \sum_{x_{i} \in R_{2}} y_{i} \]

回归树但看公式可能有些困难，最好找道例题或者自己敲遍代码加强理解。另外cart算法也容易过拟合，需要配合减枝。

6.随机森林

树看起来内容差不多了，但有很多树的时候，就形成了森林。为什么需要很多树？这是因为我们在处理问题时可能会不知道那些特征是有用的，那些特征是没有用的，为此不妨多训练几颗树，让每个树的特征随机选取。最后通过统计所有树的输出结果少数服从多数得到答案。

随机森林的结构简单而高效，当不知道用什么算法时不妨试试随机森林。而且这类集成学习的方法也不单单适用于决策树，同时也可以集成神经网络。

7.Boosting算法

Boosting是提升的意思，Boosting算法是通过把弱学习器加强成强学习器。一个典型的例子是GBDT算法

GBDT全称是Gradient Boosting Decision Tree，它利用CART的回归树作为弱学习器。这里只给出实现思路，具体公式暂不呈现。

我们引入一个残差的概念，它指的是模型的预测值和真实值的差距。当我们训练了一个树，它的输出结果会与真实值存在残差，我们可以再训练一个树来预测残差，当然这个预测残差的树也必然会与真实残差存在一个残差。不过没关系，我们可以套娃，套到结果可以接受的样子，大概的思路类似梯度下降法，同时公式也是用的一阶导数（负梯度）来近似残差。

另外还有XGBoost算法，XG是Extreme Gradient的意思，XGBoost在GBDT的基础上又做了改进，使用了二阶导数的信息，同时又加了一个正则项来防止过拟合。