opencv-python学习(5)--傅里叶变换与小波变换
摘要
opencv的python图像处理学习笔记
从空间基的角度介绍小波变换
1. 信号的数学表示
人类探索自然的工具是数学,为此探索的第一步就是将现实中的事物映射到数学上。
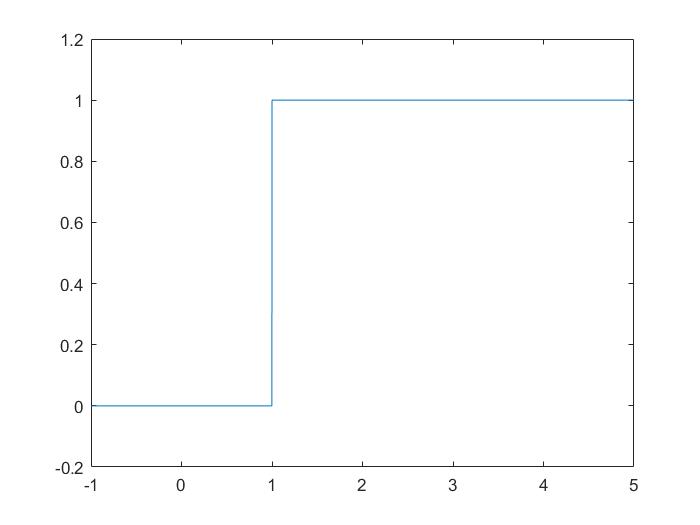
函数就是很好的工具,甚至可以将抽象的数学用图像的方法在坐标系中表示出来。比如一个阶跃信号,被表示为了一个幅值随时间变化的函数。它可以在平面直角坐标系中表示出来,其中横坐标代表时间,纵坐标是幅值。
2.距离与度量空间
上面这图是使用Matlab绘制的,看着是连续的线,但实际上只是先绘制了一些离散的点,然后连接成线的。
平面上的点\(p_1\)由两个坐标构成,一个是时间\(x_1\),一个是幅值\(y_1\)
平面集合中的两个元素\(p_1,p_2\),在数学上可以引入距离的概念,定义为\(d(p_1,p_2)\),该距离函数被称为空间集合上的度量,有距离函数的空间集合就称为度量空间。
这里为便于理解就不给出严格的数学定义,下同。
3.范数与赋范空间
有了度量函数就可以度量距离了,但是对于单个点的距离或者说是向量还没有办法度量。
如果你认为和零点的距离不就是向量的距离吗,那非常好,这个空间的范数就已经被定义了,拥有范数函数的空间集合就称为赋范空间。
显而易见赋范空间应该包含于度量空间。
4.线性空间、内积空间与正交性
线性空间的概念就非常熟悉了,满足加法的交换律结合律,乘法的分配律等就是线性空间,线性空间的好处在于任何一个元素都可以使用一组基来线性表示。
对于一个线性赋范空间,如果赋予它内积的运算,它就被称为内积空间,这个运算的数学上的意义是为了能将矢量转换为标量,显而易见内积空间应该包含于线性赋范空间。
当两个向量的内积为0时,这两个向量相互正交,如果一组基两两正交,则称这组基是正交基。
5.希尔伯特空间
对于上图信号所处的空间来说,是一个简单的二维线性内积空间,其中维度就是指需要多少个值来描述空间中的一个元素。
因为它的坐标集合是实数集,所以这个空间又是完备的,有限维度的完备内积空间被数学家称为欧几里德空间。(完备性要求度量空间中的所有柯西序列都收敛于该空间的一点)
一个有限维度的空间只能表达低于该维度的函数,比如在平面直角坐标系中只能表示一维函数,曲面就需要在三维欧几里德空间中才能画出来。
维度是一方面的局限,另一个可以简化问题的决策在于基的选择。同样是二维的欧几里德空间,表示一个半径为1的圆,使用 \(x\),\(y\)方向的单位向量作为基底,可以写作\(x^2+y^2=1\),而在极坐标下只需要写\(r=1\)
假如有一个空间是无限维的,同时有很多基底供你选择,这样一个空间是不是很棒呢?实际上这也是科学家一直在努力的方向。一个维度不受限的欧几里德空间被称为希尔伯特空间。
6.傅里叶变换与短时傅里叶变换
希尔伯特空间维度是任意的n维,坐标轴的取值也可以从实数拓展到虚数,人类无法想象这个空间,但数学可以将它抽象出来。为方便理解,我们还是以欧几里德空间来想象它。
有了希尔伯特空间算是解决的第一个问题,无限维的好处是特征有无限多,任何的低维信号在希尔伯特空间都可以映射成向量。现在需要选取一些合适的基,最好的最容易理解和接受的基仍然是沿着假想中的坐标轴的单位向量。
其次是傅里叶提出的三角函数正交基,三角函数的正交性证明感兴趣的可以见参考资料[4]
傅里叶变换的本质就是在希尔伯特空间换了一组基来表示一个信号。为了区分,把以时间方向为基的表示称为时域表示,三角函数基称为频域表示。这一对表示有着非常有意思的性质,他们互为倒空间,在时域上极短的信号体现在频域上就是无限长,反过来也一样。
傅里叶变换很好用,但同时也有它的局限性,因为过多关注了频域,对于时域的信息反而获取不到。对于特定的情况,傅里叶变换后的信号可能没这么容易获取信息。
比如对于一个频率随时间变换的信号,出来的图像如图,上图表示时域信号,下图为频域信号
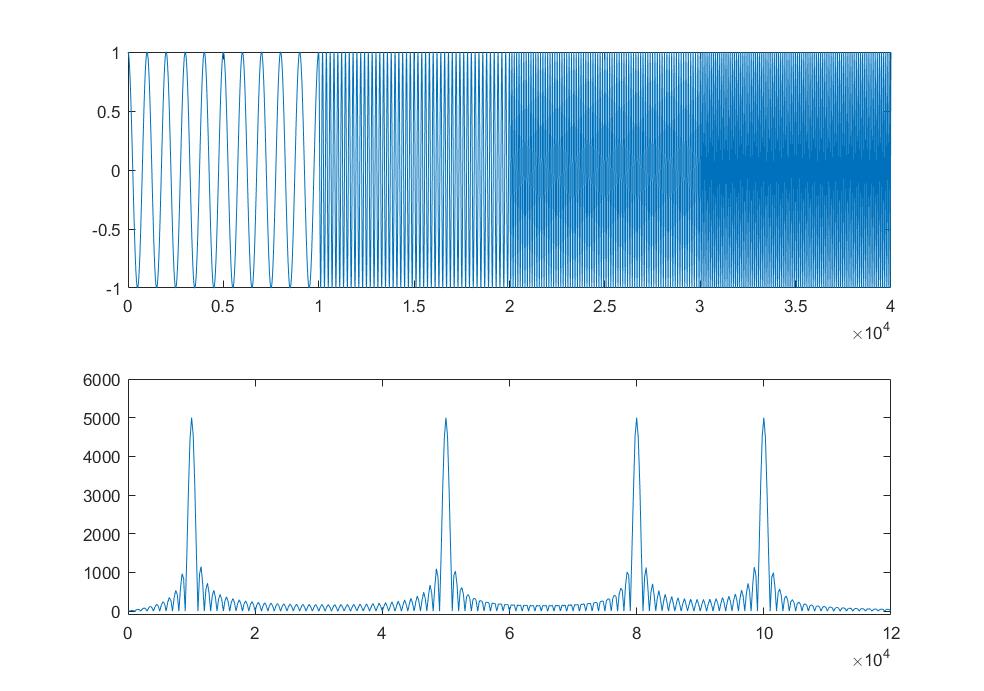
可以看出频谱除了有4个比较明显的峰外还有许多振荡,而且没法体现出在时域信号中频率随时间变化这一显著的特点。
所以为了解决这一问题,短时傅里叶变换被提了出来。既然时间信息丢失了,那就补上,短时傅里叶变换和傅里叶变换唯一的区别在于多了一个窗口函数,用一个窗函数去框选时域信号,然后对这一部分再做傅里叶变换,这体现在空间中就是多了一个维度,用热力图来表示如下。
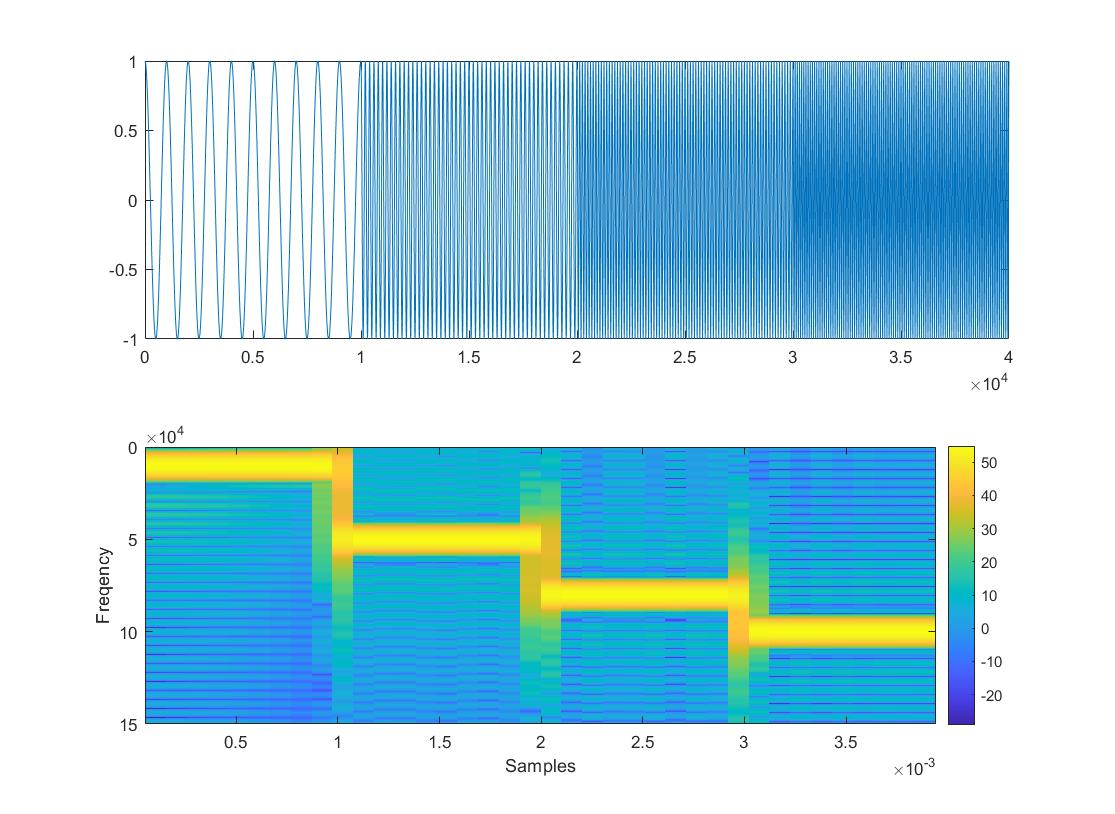
短时傅里叶变换就很明显的表现出了时间上的频率变换,但问题在于要怎么知道这个窗口选多大才是合理的,选大了就会出现和傅里叶变换一样的问题出现时域信息丢失,选小了会让频域上的分辨率降低,这里倒是有点测不准原理的感觉了。
7.小波变换
不知道该多大的窗口那不如把窗口也变为可变的,不过这样一来,维度又会多了一维,在三维空间里就显得失去了直观性。再往深了考虑的解决方法是使用自适应短时傅里叶变换,使用算法来让窗口自适应信号。
不过也可以换个角度思考,现在陷入瓶颈的原因还是在于使用了两个互为倒空间的基,出现了测不准的问题,如果重新在希尔伯特空间选择一个基,是否就能够解决这个问题。
首先波这个概念很好,有了波才引出了频域,我们希望保留它。其次加窗的想法也很好,它保留了时域的信息,这两者都是有物理意义的。这样我们是否能够使用一个小范围的波来作为基呢?起个名字就叫小波,用\(\psi(t)\)来表示。,样子大概如下。
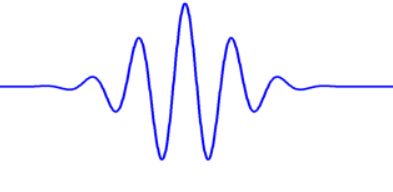
当然这只是一个概念图,光有一个波可构不成希尔伯特空间的基。
好在我们是在线性空间里讨论的,只要一个集合能被一组已知的基完全线性表示,那这个集合也是一组基。这里完全线性表示的意思是用上了所有的元素才能表示全。
所以只要加上尺度变换\(\frac{1}{\sqrt{a}}\psi(\frac{t}{a})\),这样随着a的变换,在时域上看是变胖变瘦,在频域上看是遍历所有频率。前面的系数是为了归一化,同样为了方便处理,我们人为将小波在时域上的积分设置为0,这样就和三角函数相统一了。
解决了基的问题,好像顺带也把频域的特性提取问题解决了,因为小波基底的选择就是借用的波的概念,下一步是让波在时域上动起来,这个也很好处理,只要用初中学的函数平移就行。以小波为基底的变换就叫小波变换。下面直接给出函数\(f(t)\)小波变换的完整公式。
\[ W T(a, \tau)=\frac{1}{\sqrt{a}} \int_{-\infty}^{\infty} f(t) * \psi\left(\frac{t-\tau}{a}\right) d t \]
实际上小波不一定长得和上图一样,尺度变换也可以用其他方法表示,记作\(\phi(t)\)
小波的函数\(\psi(t)\)被称为母小波,尺度函数\(\phi(t)\)被称为父小波。确定了两者就可以愉快地进行小波变换了!
参考资料
[1] 卷积神经网络的底层是傅里叶变换,傅里叶变换的底层是希尔伯特空间坐标
[3] 欧几里得空间与希尔伯特空间