opencv-python学习(2)--灰度变换与直方图

发表于 2022-10-17 更新于 2022-12-10 分类于学习笔记，计算机本文字数： 4.4k 阅读时长 ≈ 4 分钟

摘要

opencv的python图像处理学习笔记

1.灰度变换

1.1 灰度化

灰度化是将图片由RGB三通道转为只有灰度的单通道图片。

改变颜色空间使用cvtColor(input_image, flag) BGR↔︎灰色和BGR↔︎HSV的转换比较常用，这里主要看灰度图

cv2.cvtColor(image,cv2.COLOR_BGR2GRAY)

def trun_gray(img):
    try:
        depth = img.shape[2]
        if depth == 3:
            return cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
    except IndexError:
        return img

1.2 二值化

二值化是将图片矩阵转为只有0和255的图片

1
2
3

cv2.threshold(src, thresh, maxval, type)

ret,binary = cv2.threshold(img,0,255,cv2.THRESH_BINARY + cv2.THRESH_OTSU)

传入源图片src，阈值thresh，最大值maxval，参数type，cv2.THRESH_OTSU指使用OTSU算法自动获取阈值，THRESH_BINARY等参数见下

返回ret是OTSU算法得到的阈值，binary是二值化后的图片

名称	含意
cv2.THRESH_BINARY	像素灰度值小于阈值全为0,大于阈值全为255
cv2.THRESH_BINARY_INV	像素灰度值小于阈值全为255,大于阈值全为0
cv2.THRESH_TRUNC	像素灰度值小于阈值不变,大于阈值变为阈值
cv2.THRESH_TOZERO	像素灰度值小于阈值不做任何改变,大于阈值全为0
cv2.THRESH_TOZERO_INV	像素灰度值小于阈值全为0,大于阈值不做任何改变

1.3 图像反转

图像反转又称反色变换，记原图像矩阵为r，灰度范围为[0，L-1]

反转后图像公式如下 \[ s = L-1-r \]

如果是二值图就相当于黑白反转

def image_inverse(x):
    value_max = np.max(x)
    y = value_max - x
    return y

1.4 对数变换

通用变换规律 \[ s = c \cdot \ln(1+r) \]

其中加1是为了确保输出的值都大于0 对数通常以e为底。

变换是为了让图片的动态显示范围更直观，在实际展示时还要注意归一化。一个典型的用处就是展示傅里叶频谱图，频谱的低频值比较重要。

# 归一化映射函数
def normImg(self,x):
    return  cv2.normalize(x,None,0,255,cv2.NORM_MINMAX)

def log_image(self):
  img = self.image
  log = np.uint8(self.normImg(self,np.log(1.0 + img)))

1.5 伽马变换

伽马变换又称幂律变换，可以提升暗部细节，对过白或过暗的图片进行矫正。

基本形式为

\[ s = c (r + \epsilon)^\gamma \]

其中补偿系数\(\epsilon\)一般为0

同样伽马变换也要注意映射到指定范围

def gamma_image(self):
  img = self.image
  gamma = np.power(img, eps)
  gamma = np.uint8(normImg(self,gamma))

\(\gamma\)大于1是增强暗度，小于1是增强亮度。

1.6 分段线性变换

1.6.1 对比度拉伸

没啥好说的，就是再映射

1.6.2 灰度级分层

当只对某一范围的灰度感兴趣时，我们可以将该区域设置为白色或黑色，其他保持不变或变为另一种颜色。这样可以提取出想要的信息。

1.6.3 比特屏幕分层

对于256级的8位灰度图，将每一位的灰度拆分出来，生成对应的二值图像，并将不同层次的灰度二值图像组合可以在不损失图像精度的前提下降低图像存储空间。

第1位，二值图像灰度值为1的灰度级区间为[2^0, 2^1) , 即 [0, 2);

第2位，二值图像灰度值为1的灰度级区间为[2^1, 2^2), 即 [2, 4);

...

第8位，二值图像灰度值为1的灰度级区间为[2^7, 2^8), 即 [128, 256) 。

2.直方图

2.1 opencv中的直方图

直方图是指把像素值（通常为[0,255]）的像素点个数统计出来画成直方图

# 展示直方图
def show_image_hist(self):
    if len(self.image.shape) == 2:
        # hist = cv2.calcHist([self.image],[0],None,[256],[0,256])
        plt.hist(self.image.ravel(),256); 
    else:
        color = ('b','g','r')
        for i,col in enumerate(color): 
            histr = cv2.calcHist([self.image],[i],None,[256],[0,256]) 
            plt.plot(histr,color = col) 
            plt.xlim([0,256])
    plt.show()

其中.ravel()是将矩阵拍成一维数组

cv2.calcHist(images,channels,mask,histSize,ranges)是opencv的直方图接口，api参数如下

images：原图像当传入函数时应用中括号[]括起来，如[img]
channels：如果输入图像是灰度图，它的值就是[0]；如果是彩色图，传入的参数可以是[0],[1],[2]，分别对应通道B、G、R
mask：掩膜图像。统计整张图像的直方图就把它设置为None。当统计图像某一部分的直方图时，需要自己制作一个掩膜图像
histsize：BIN的数目。用中括号[]括起来，如[256]
ranges：像素值范围，通常为[0, 256]

直方图均衡化也可以作为提高图像对比度的一个手段。下面给出一个opencv自带的均衡函数dst = cv2.equalizeHist(img)但通常这样操作效果不是很好，还需要考虑全局的信息，为解决该问题，需要使用自适应的直方图均衡化。该方法会将图片切成小块，进行均衡。但直接这样会让噪声也扩撒，所以在切成小块前要先把超过对比度上限的像素点均匀分散到其他bins上。

自适应直方图均衡化的opencv API是cv2.createCLAHE(clipLimit, tileGridSize)

clipLimit：对比度限制，默认是40
tileGridSize：分块的大小，默认为8*8

1
2
3

# 创建一个自适应均衡化的对象，并应用于图像
clahe = cv.createCLAHE(clipLimit=2.0, tileGridSize=(8,8))
cl1 = clahe.apply(img)

2.2 直方图均衡原理

以灰度图像为例，它的直方图（不同灰度的像素点个数统计）的积分和为总像素点的个数，图像的灰度变量记为r。然后在其经过一个灰度变换\(T(r)\)后，我们记为s，可知s的总像素个数应该与r相同，也就是说s的直方图积分等于r的直方图积分。同时将s和r归一化（横坐标由[0,L-1]映射到[0,1]，直方图的面积设置为1），这条定理也应该成立，公式如下：

\[ \int_{0}^{b} p_{s}(s) d s=\int_{0}^{a} p_{r}(r) d r \]

其中\(a=b=1\),\(p_s\)和\(p_r\)分别为s和r的直方图函数，因为已经进行了归一化，它们的积分(面积)为1，这样也可以将\(p\)看做是图像的概率密度分布函数。反正在计算机眼里，图片只是一些随机分布的噪点罢了。

另一方面，如果灰度变化函数是单调递增的函数，那么当\(b=T(a)\)时，该公式也应当成立。给一个直观的参考图。

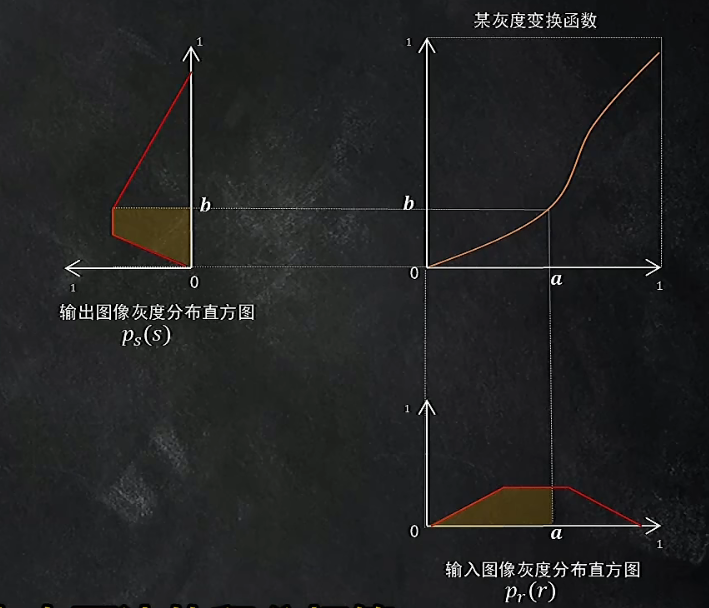
将上式改为微分形式(两边对s求导)有：

\[ p_{s}(s)=\frac{p_{r}(r) d r}{d s} \]

想要让变化后的图片实现直方图均衡，即让\(p_s\)恒等于1，代入可得

\[ p_{r}(r)=\frac{d s}{d r} \]

两边再对r积分得到

\[ s=\int_{0}^{x} p_{r}(r) d r \]

再将积分转换为离散的像素点的求和，最后别忘记了反归一化

\[ s_{k}=(L-1)*\sum_{i=0}^{k} p_{r}(i) \]

这样我们就得到了输出图像灰度变量s，利用直方图巧妙地得到了灰度变化函数。再通过灰度变化函数对原图的像素点进行操作即可得到输出图像。

2.3 直方图规定化

有时候均衡不是我们想要达到的目的，比如一个哥特风的cos照，均衡化后反而变亮了，失去了原有的风格。但原图拍摄的又比较暗，无法看清细节。所以我现在希望能将目标图像的直方图转变为我想要的直方图以实现图像变换的效果。

下面简单介绍原理，我们知道对于归一化的图像灰度变量a有

\[ s=T(a) = \int_{0}^{x} p_{a}(a) d a \]

其中s是归一化平衡化直方图的灰度变量，它的概率密度函数恒为1 \(T\)是a到s的灰度变换函数。

那同样对于我们需要的目标图像的灰度变量b，它所对应的平衡直方图也应该是s

\[ s=G(b) = \int_{0}^{x} p_{b}(b) d b \]

其中\(G\)是b到s的灰度变换函数。

这里理一下思路：

我们现在可以从目标图像B的灰度直方图中得出灰度变换函数\(G\)、还可以从原图像A中得到均衡后的图像\(A^{'}\)，并且已知目标图像B的均衡后的图像\(B^{'}\)有\(B^{'}=A^{'}\)

现在的问题明确了，只要知道了\(G^{-1}\)就可以由\(B^{'}\)获得目标图像B。但问题在于这个反函数没有这么容易求。不过在工程上倒是有一个近似方法，利用\(G\)可以将[0,L-1]范围的像素先做一个映射表。然后通过遍历均衡后图像的像素点通过查表法映射回去。虽然不知道函数，但对于离散值，这样的计算也是足够了。

参考资料

[1] https://blog.csdn.net/XWMRHZZ/article/details/124393745

[2] https://blog.csdn.net/my_cat__/article/details/125477831

[3] opencv官方手册

[4] https://blog.csdn.net/m0_47472749/article/details/114223563

[5] https://blog.csdn.net/gg13213/article/details/123671416

[6] 【手写图像处理库4】别再说数学理论鼓噪无味了，概率论的典型应用，直方图均衡化，一键完成对比度增强，懒人神器，数字图像处理，冈萨雷斯