密度泛函理论-泛函

发表于 2022-05-27 更新于 2022-12-10 分类于学习笔记，物理本文字数： 3k 阅读时长 ≈ 3 分钟

摘要

泛函简介，从费马原理出发利用泛函介绍了光为什么沿直线传播，光的折射定律。

1.什么是泛函？

如果一个函数的变量也是一个函数，则称为泛函。

泛函就是函数的函数。

2.泛函有什么用？

我们都知道微分是指函数(f(x))在某一点处（dx\(\approx\)无穷小）的变化量。

泛函的微分那就不能叫这么土的名字了，得换个有b格的名字，叫做变分，泛函的自变量也得换个名字叫宗量

提到变分，肯定绕不开大名鼎鼎的变分法，变分法讲的最多的是最速降线的问题，但实际上伯努利的解法参考了光学中的费马原理。

费马原理说的是：过两个定点的光总走光程的一阶变分为零的路径。[2]

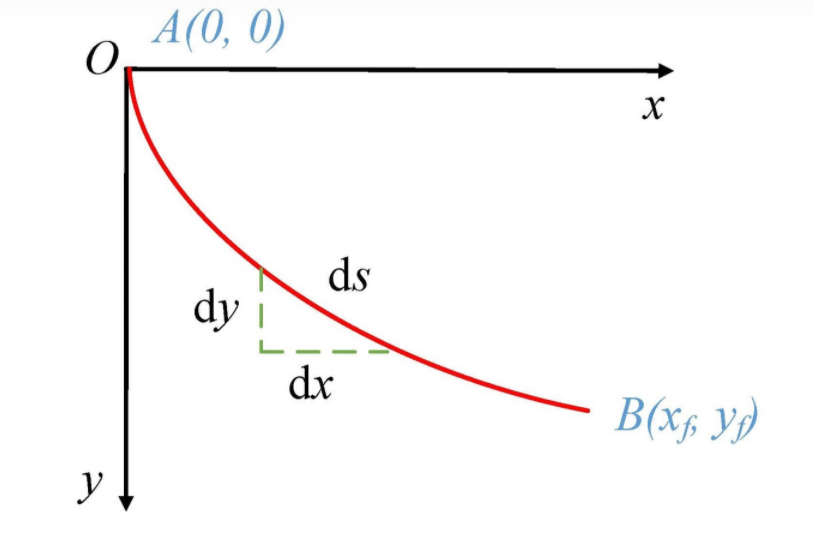
图来自参考资料[3]

假设在xy平面存在折射率为n(y)的介质（这里可以理解为有很多层不同的介质）光线从原点出发，会选择走那条路径？

我们都知道光程是折射率乘光线在介质中走过的路程，所以有光程S为： \[ \begin{aligned} S &=\int n(y) \sqrt{(d x)^{2}+(d y)^{2}} \\ &=\int n(y) \sqrt{1+\left(\frac{d y}{d x}\right)^{2}} d x \\ &=\int n(y) \sqrt{1+\left(y^{\prime}\right)^{2}} d x \end{aligned}\tag{1} \]

我们令 \[ L\left(y, y^{\prime}\right) = n(y) \sqrt{1+\left(y^{\prime}\right)^{2}}\tag{2} \]

又因为是从A点积分到B点，光程可以表达为下述简洁的模式： \[ S = \int_{A}^{B} d x L\left(y, y^{\prime}\right)\tag{3} \]

光经过的路线可以写作\(y=f(x)\)这样一个函数，可以看出光程S是以y为宗量的泛函，所以只要将光程的一阶变分写出来，根据费马原理它等于0，求解出\(f(x)\)就解完了。

所以一阶变分怎么写呢？我们知道变分是泛函的微分。微分是函数的微小变化，先看宗量如果发生了微小变化\(\delta y(x)\)

那么 \[ \delta L\left(y, y^{\prime}\right) = \frac{\partial L}{\partial y} \delta y+\frac{\partial L}{\partial y^{\prime}} \delta y^{\prime}\tag{4} \]

光程的变分为 \[ \begin{aligned} \delta S[y(x)] &=\int_{A}^{B} d x \delta L\left(y, y^{\prime}\right) \\ &=\int_{A}^{B} d x\left[\frac{\partial L}{\partial y} \delta y+\frac{\partial L}{\partial y^{\prime}}(\delta y)^{\prime}\right] \\ \end{aligned}\tag{5} \]

上式第二项中可以写作\(\frac{\partial L}{\partial y^\prime} \frac{\mathrm{d}(\delta y)}{\mathrm{d} x}\)对该项使用分部积分得

\[ \begin{aligned} \int_{A}^{B} \frac{\partial L}{\partial y^{\prime}} \delta y^{\prime} \mathrm{d} x &=\int_{A}^{B} \frac{\partial L}{\partial y^{\prime}} \mathrm{d}(\delta y) \\ &=\left.\frac{\partial L}{\partial y^{\prime}} \delta y\right|_{A} ^{B}-\int_{A}^{B} \delta y \frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{\partial L}{\partial y^{\prime}}\right) \mathrm{d} x \end{aligned}\tag{6} \]

又因为断点固定所以有两段变分为零。即 \[ \delta y(A)=\delta y(B)=0\tag{7} \]

代入回式(5)有 \[ \delta S[y(x)]=\int_{a}^{b} d x\left[\frac{\partial L}{\partial y}-\frac{d}{d x}\left(\frac{\partial L}{\partial y^{\prime}}\right)\right] \delta y \tag{8} \]

要想让光程的变分为0，则有 \[ \frac{\partial L}{\partial y}-\frac{d}{d x}\left(\frac{\partial L}{\partial y^{\prime}}\right) = 0\tag{9} \]

注意，我这里始终没有把L的具体函数代入，也就是说这个方程是一个通用的方程。实际上这就是著名的欧拉-拉格朗日方程。费马原理其实是物理中的最小作用量原理。利用变分法我们就可以在物理学世界嘎嘎乱杀。比如说

2.1 光在均匀介质中走的是直线

我们有\(n(y)=n\)，\(L=n\sqrt{1+\left(y^{\prime}\right)^{2}}\)可得

\[ \frac{\partial L}{\partial y}=0, \quad \frac{\partial L}{\partial y^{\prime}}=\frac{ny^{\prime}}{\sqrt{1+y^{\prime 2}}}\tag{10} \]

代回公式(9)

\[ \frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{ny^{\prime}}{\sqrt{1+y^{\prime 2}}}\right)=0\tag{11} \]

显而易见解为\(y(x) = k x+c\)是一条直线，

2.2 光的折射定律

光为什么会发生折射，我们现在知道了光在均匀介质中沿直线传播，假设光平行于xy平面入射介质在\(y=0\)处交接，设光线在x轴的交点为\((x,0)\)，则点AB间的光程可以写作。

\[ \begin{aligned} S & = n_{1} \sqrt{y_{1}^{2}+(x-x_1)^{2}}\\ & + n_{2} \sqrt{y_{2}^{2}+(x_2-x)^{2}} \end{aligned}\tag{12} \]

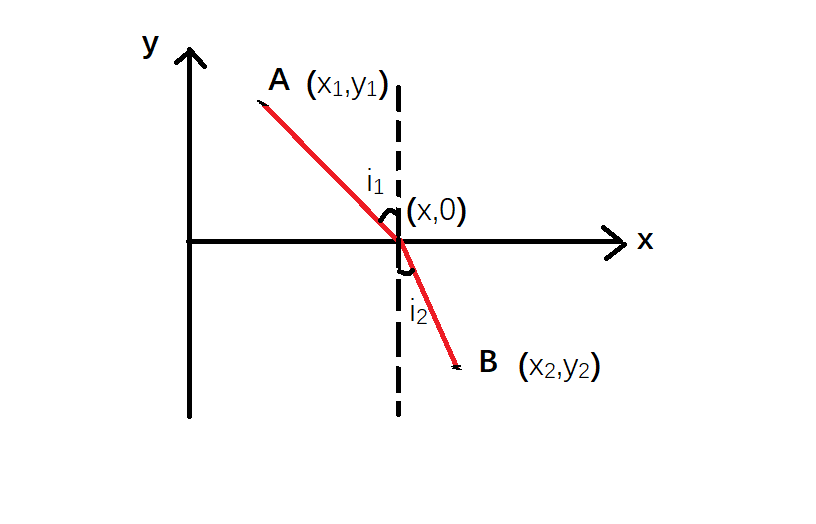
光程的变分为零即为\(\frac{dS}{dx} = 0\)

\[ \begin{aligned} \frac{d S}{d x} & = n_{1} \frac{x-x_{1}}{\sqrt{y_{1}^{2}+\left(x-x_{1}\right)^{2}}}\\ &- n_{2} \frac{x_{2}-x}{\sqrt{y_{2}^{2}+\left(x_{2}-x\right)^{2}}} \\ & = 0 \end{aligned}\tag{13} \]

所以有 \[ n_{1} \sin i_{1}-n_{2} \sin i_{2}=0\tag{14} \]