使用紧束缚近似绘制多层黑磷能带图

发表于 更新于 分类于 ， 本文字数： 5.1k 阅读时长 ≈ 5 分钟

摘要

紧束缚近似下使用二次量子化表示黑磷哈密顿量并利用 python编写代码绘制黑磷能带图。

1.单层及基础原理

使用紧束缚近似绘制单层黑磷能带图

2.双层黑磷的能带结构

这里双层是指最常见的AB型堆垛方式的双层，其正面图及俯视图如下图

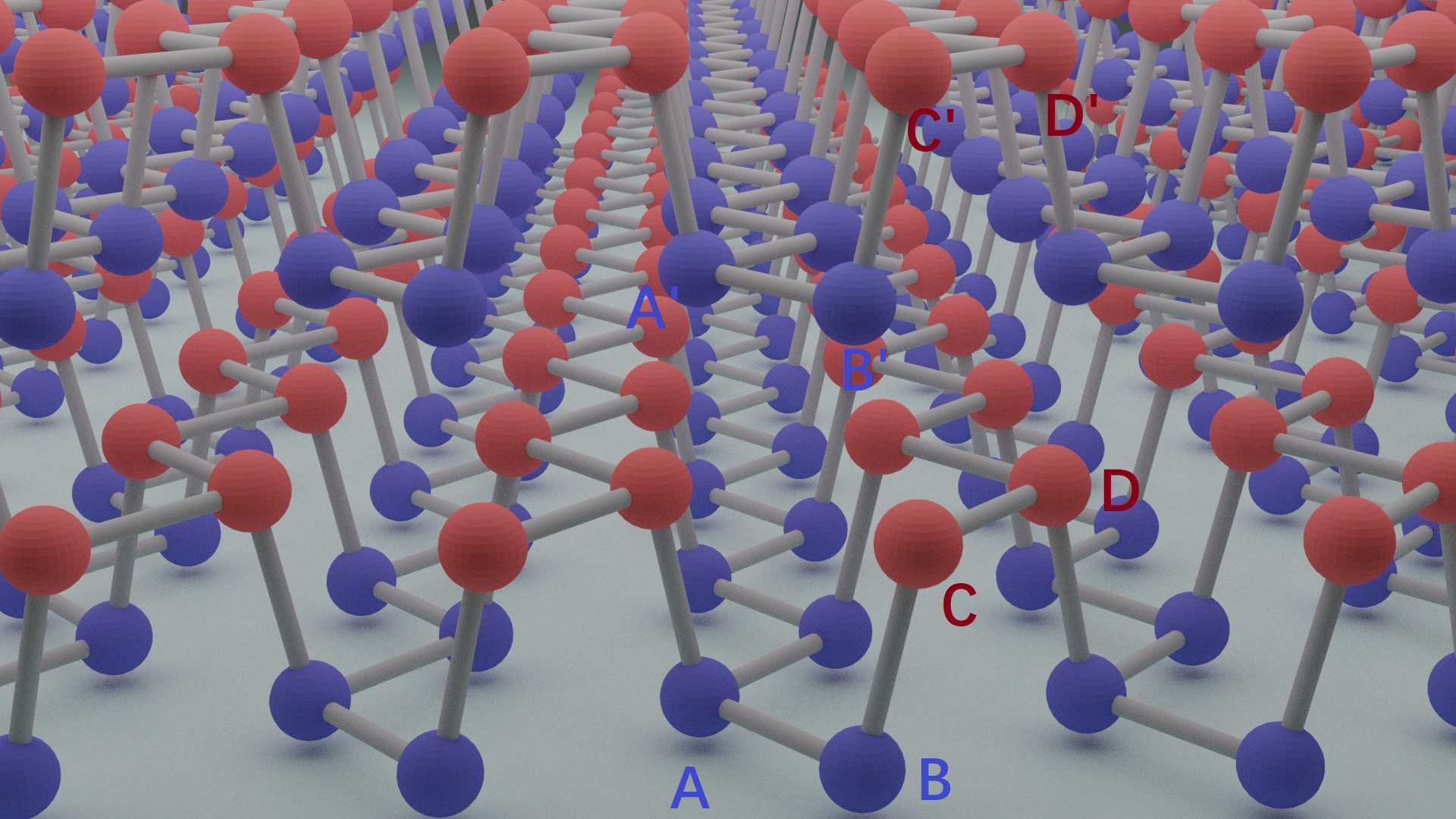
双层黑磷原子结构图
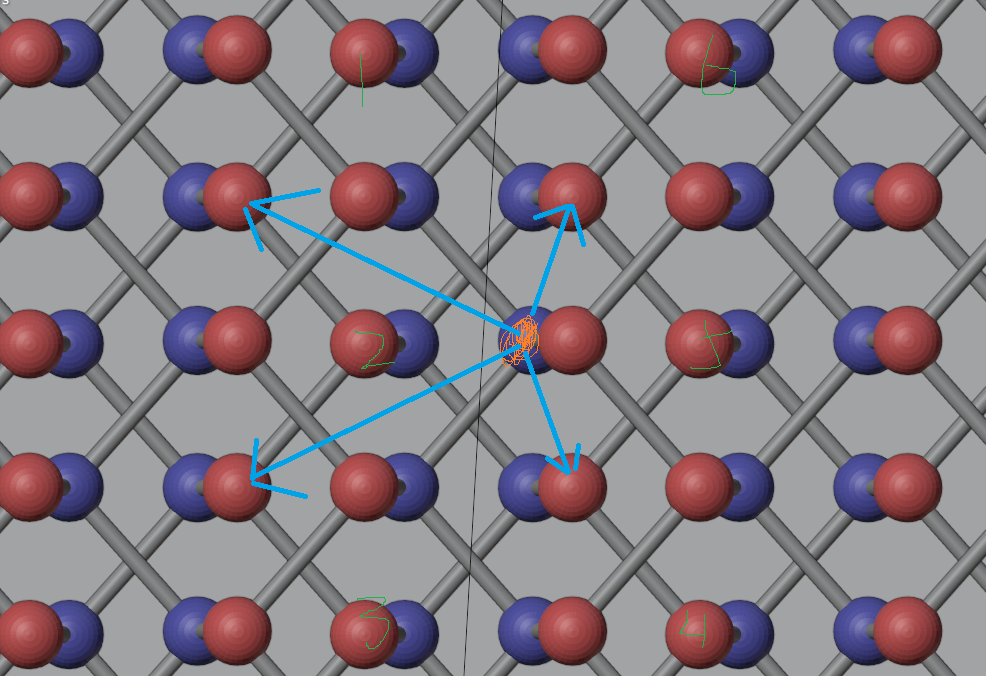
双层黑磷俯视图

下层的原子仍然标记为ABCD，上层的原子标记为A'B'C'D'

俯视图中给出了上下层间的跳跃项。其中只考虑上层中的蓝色原子A'B'跳跃到下层中的红色CD。橙色的点为B'原子，记为跳跃起点，蓝色箭头是跳跃到下一层的原子C，短的跳跃参数记为\(t_1^\perp\)，长的记为\(t_4^\perp\)。绿色数字是跳跃到下一层的原子D，短的记为\(t_2^\perp\)，长的记为\(t_3^\perp\).

给出这两项的表达式

\[ \begin{aligned} t_{B C}^{\prime}(k)=& 2 t_{1}^{\perp} \cos \left[k_{y} a_{1} \sin \left(\alpha_{1} / 2\right)\right] \times \exp \left[i k_{x} a_{2} \cos \beta\right] \\ &+2 t_{4}^{\perp} \cos \left[k_{y} a_{1} \sin \left(\alpha_{1} / 2\right)\right] \times \exp \left\{-i k_{x}\left[2 a_{1} \cos \left(\alpha_{1} / 2\right)+a_{2} \cos \beta\right]\right\} \end{aligned}\tag{1} \]

\[ \begin{aligned} t_{B D}^{\prime}(k)=& 4 t_{3}^{\perp} \cos \left[k_{y} 2 a_{1} \sin \left(\alpha_{1} / 2\right)\right] \times \cos \left\{k_{x}\left[a_{1} \cos \left(\alpha_{1} / 2\right)+a_{2} \cos \beta\right]\right\} \\ &+2 t_{2}^{\perp} \cos \left\{k_{x}\left[a_{1} \cos \left(\alpha_{1} / 2\right)+a_{2} \cos \beta \right] \right\} \end{aligned}\tag{2} \]

以8个原子的电子波函数为基底写出双层黑磷的哈密顿量如下

\[ H_{b i}=\left(\begin{array}{cc} H & H_{c} \\ H_{c}^{\dagger} & H \end{array}\right)\tag{3} \]

其中H是单层黑磷的哈密顿量，

\[ H_{c}=\left(\begin{array}{cc} 0 & 0 \\ H_{2} & 0 \end{array}\right)\tag{4} \]

上式中

\[ H_{2}=\left(\begin{array}{ll} t_{B D}^{\prime}(k) & {t_{B C}^{\prime}}^{*}(k) \\ t_{B C}^{\prime}(k)& t_{B D}^{\prime}(k) \end{array}\right)\tag{5} \]

使用python编写程序,其实只是在上一个程序上稍加修改。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
from para import *
import cmath
import matplotlib.pyplot as plt

def ham(kx,ky):
    tab = 2*t1*np.cos(ky*a1*np.sin(alpha1/2))*cmath.exp(1j*kx*a1*np.cos(alpha1/2))+\
        2*t3*np.cos(ky*a1*np.sin(alpha1/2))*cmath.exp(-1j*kx*(a1*np.cos(alpha1/2)+2*a2*cos_beta))
    tcb = t2*cmath.exp(-1j*kx*a2*cos_beta) + t5*cmath.exp(1j*kx*(2*a1*np.cos(alpha1/2)+a2*cos_beta))
    tdb = 4*t4*np.cos(ky*a1*np.sin(alpha1/2))*np.cos(kx*(a1*np.cos(alpha1/2)+a2*cos_beta))

    tbc = 2*t1p*np.cos(ky*a1*np.sin(alpha1/2))*cmath.exp(1j*kx*a2*cos_beta) + 2*t4p*np.cos(ky*a1*np.sin(alpha1/2))*cmath.exp(-1j*kx*(2*a1*np.cos(alpha1/2)+a2*cos_beta))
    tbd = 4*t3p*np.cos(ky*2*a1*np.sin(alpha1/2))*np.cos(kx*(a1*np.cos(alpha1/2)+a2*cos_beta)) + 2*t2p*np.cos(kx*(a1*np.cos(alpha1/2)+a2*cos_beta))

    h0 = np.zeros((2, 2), dtype=complex)
    h1 = np.zeros((2, 2), dtype=complex)
    hm = np.zeros((4, 4), dtype=complex)
    h2 = np.zeros((2, 2), dtype=complex)
    hc = np.zeros((4, 4), dtype=complex)
    hb = np.zeros((8, 8), dtype=complex)

    h0[0,0] = 0
    h0[1,1] = 0
    h0[0,1] = tab
    h0[1,0] = h0[0,1].conj()

    h1[0,0] = tdb
    h1[1,1] = tdb
    h1[0,1] = tcb
    h1[1,0] = h1[0,1].conj()

    h2[0,0] = tbd
    h2[1,1] = tbd
    h2[1,0] = tbc
    h2[0,1] = h2[1,0].conj()

    hm[:2,:2] = h0
    hm[2:,2:] = h0
    hm[:2,2:] = h1
    hm[2:,:2] = h1

    hc[2:,:2] = h2

    hb[:4,:4] = hm
    hb[4:,4:] = hm
    hb[:4,4:] = hc
    hb[4:,:4] = hc.T.conj()


    return hb

def Draw_1d(kx, ky, eig, n_step):
    """画图函数"""
    # 计算带隙
    Conduction_bottom = np.min(np.where(eig > 0, eig, np.inf))
    Valence_top = np.max(np.where(eig < 0, eig, -np.inf))
    print("带隙为",Conduction_bottom-Valence_top)
    dim = eig.shape[-1]
    for i in range(dim):
        plt.plot(kx, eig[0,:,i],'b-')
        plt.plot(ky, eig[1,:,i],'b-')
    plt.show()

def Draw_2d(kx, ky, eig, n_step):
    """画图函数"""
    fig = plt.axes(projection='3d')
    x, y = np.meshgrid(kx, ky)
    zero_plane = np.zeros((n_step, n_step))
    # 画能带图
    dim = eig.shape[-1]
    for i in range(dim):
        fig.plot_surface(x, y, eig[:, :, i], cmap='spring')
    fig.plot_surface(x, y, zero_plane, cmap='gray')
    plt.xlabel("Kx")
    plt.ylabel("Ky")
    fig.view_init(elev=2, azim=140)
    # 计算带隙
    Conduction_bottom = np.min(np.where(eig > 0, eig, np.inf))
    Valence_top = np.max(np.where(eig < 0, eig, -np.inf))
    print("带隙为",Conduction_bottom-Valence_top)
    #plt.savefig("single_BP_2D_Band.jpg", dpi=600)
    plt.show()


def main2():
    n_step = 100
    kx_list = np.linspace(-np.pi, np.pi, n_step)
    ky_list = np.linspace(-np.pi, np.pi, n_step)
    h = ham(0,0)
    size = len(h)
    two_dim_eig = np.zeros((n_step, n_step, size))

    for x in range(n_step):
        kx = kx_list[x]
        for y in range(n_step):
            ky = ky_list[y]
            h = ham(kx, ky)
            eigenvalue, eigenvector = np.linalg.eigh(h)
            two_dim_eig[x, y, :] = eigenvalue
    Draw_2d(kx_list, ky_list, two_dim_eig, n_step)


def main1():
    n_step = 1000
    kx_list = np.linspace(0, np.pi, n_step)
    ky_list = np.linspace(-np.pi, 0, n_step)
    h = ham(0,0)
    size = len(h)
    two_eig = np.zeros((2 , n_step, size))


    ky = 0 
    for x in range(n_step):
        kx = kx_list[x]
        h = ham(kx, ky)
        eigenvalue, eigenvector = np.linalg.eigh(h)
        two_eig[0, x, :] = eigenvalue
    kx = 0
    for y in range(n_step):
        ky = ky_list[y]
        h = ham(kx,ky)
        eigenvalue, eigenvector = np.linalg.eigh(h)
        two_eig[1, y, :] = eigenvalue
    Draw_1d(kx_list, ky_list, two_eig, n_step)


if __name__ == '__main__':
    main1()

3.N层黑磷的能带结构

因为仅考虑近邻项的跳跃，所以我们可以推广到N层AB型堆垛的黑磷的哈密顿量为：

\[ H_{N}=\left(\begin{array}{ccccc} H & H_{c} & & & \\ H_{c}^{\dagger} & H & H_{c} & & \\ & H_{c}^{\dagger} & H & H_{c} & \\ & & & \ddots & \\ & & & & H_{c} \\ & & & H_{c}^{\dagger} & H \end{array}\right)_{N \times N} \]

代码也差不多，但因为紧束缚的参数是通过DFT计算出能带再拟合出来的，仍使用这些参数可能会使多层的数值偏离实际值。

4.参考资料

[1] 使用紧束缚近似绘制单层黑磷能带图