使用紧束缚近似绘制单层黑磷能带图
摘要
紧束缚近似下使用二次量子化表示黑磷哈密顿量并利用 python编写代码绘制黑磷能带图。
1.黑磷的结构
黑磷作为一种新型的二维材料,不同于石墨烯的零带隙和过渡金属硫化物的低载流子迁移率。黑磷具备可以控制的直接带隙、高开关比及高载流子迁移率。因此黑磷烯也被广泛应用于光电、化学、生物等多个领域。
其具有与石墨烯类似的蜂窝型层状结构,不同之处在于黑磷的片层结构有着褶皱形态。黑磷原子结构见图1.
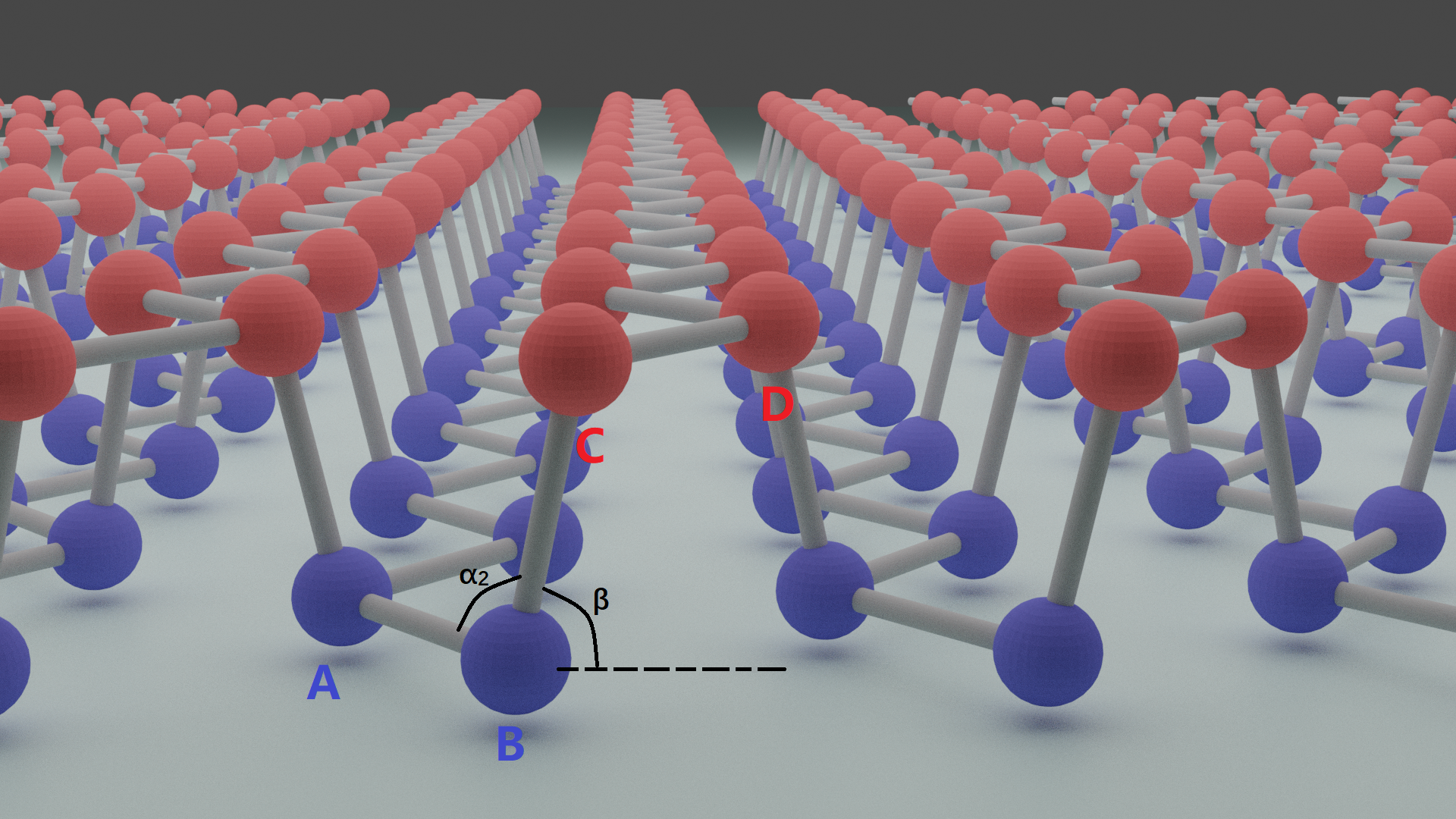
图片使用blender绘制,方法参考使用python+blender绘制原子结构示意图--以黑磷为例
黑磷的一个原胞中共有4个原子,标为ABCD,其中原子AB或者CD间的键长\(a_1=2.22 \mathring{A}\) 原子BC或AD间的键长为\(a_2=2.24 \mathring{A}\)
俯视图为六边形结构,如图2,图中另外标明了
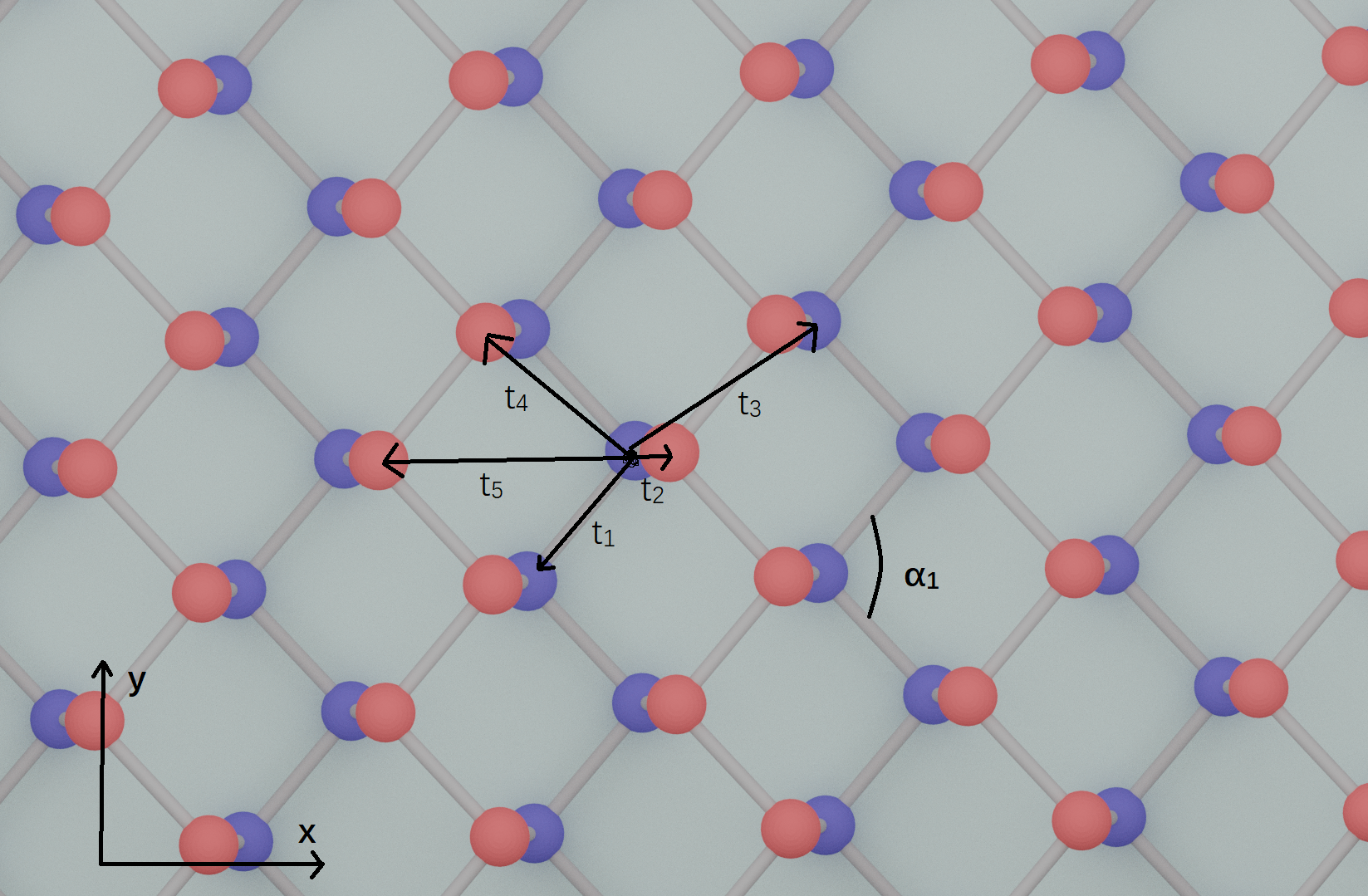
其中键角\(\alpha_2=101.9^{\circ}\), \(\alpha_1=96.5^{\circ}\), \(\cos \beta=-\cos \alpha_2 / \cos \frac{\alpha_1}{2}\)
数据来源参考资料[2](参考资料中的\(\cos \beta\)这一项应为上文表达式,给个潦草的推导。)
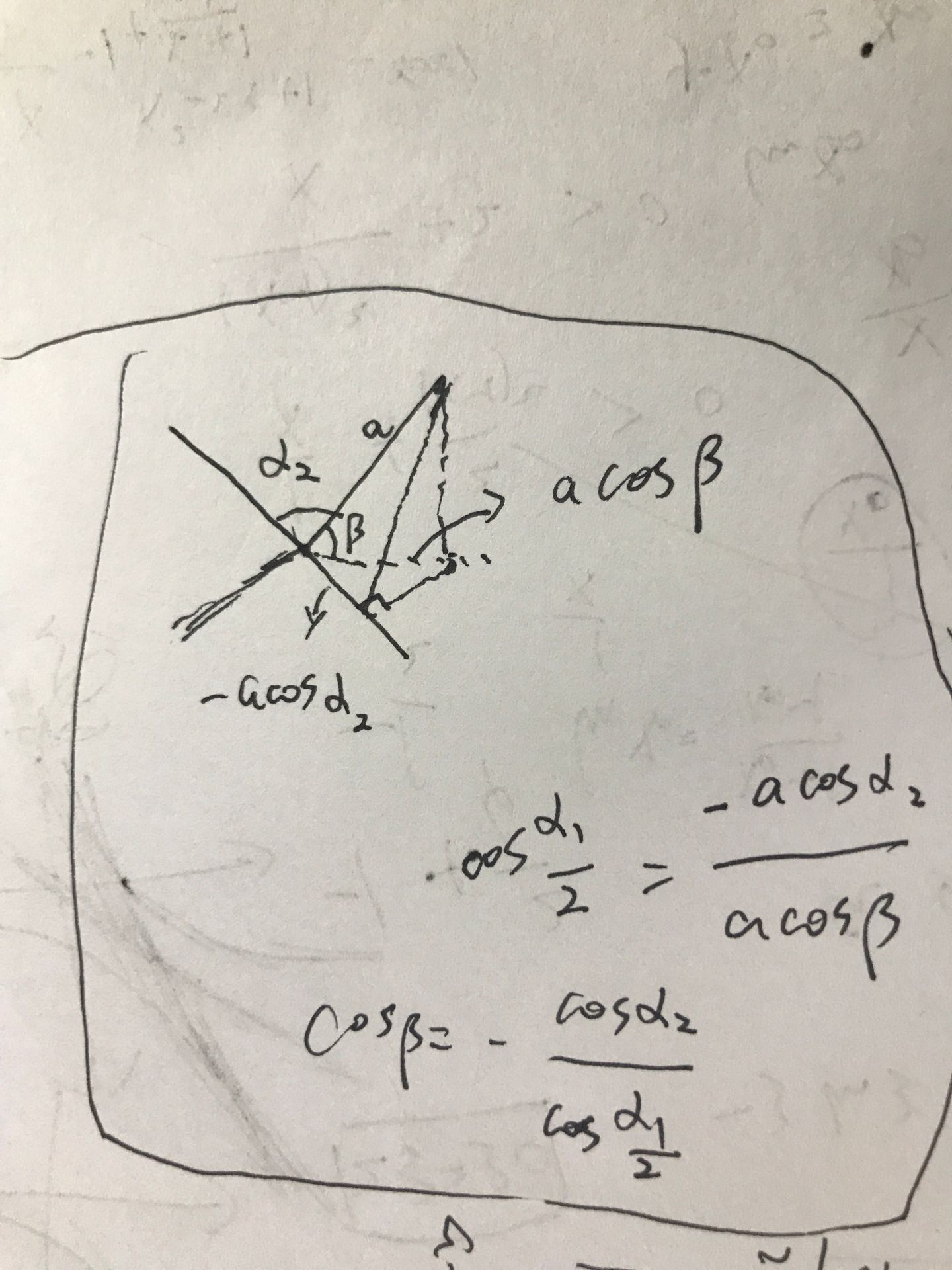
2.单层黑磷的哈密顿量
黑磷的哈密顿量可以写作 \[ H=\sum_{\langle i, j\rangle} t_{i j} c_{i}^{\dagger} c_{j} \tag{1} \]
公式(1)的含义可以间参考资料[1]
这里采用5跳近似。
先以AB原子跃迁为例,考虑近邻和次近邻共四项。由图2中\(t_1\),\(t_3\)标记所示。若以原子B为坐标原点,四个A的坐标分别为 \[ \begin{align} &A_1 = (-a_1 \cos \frac{\alpha_1}{2},-a_1 \sin \frac{\alpha_1}{2})\nonumber\\ &A_2 = (-a_1 \cos \frac{\alpha_1}{2},a_1 \sin \frac{\alpha_1}{2})\nonumber\\ &A_3 = (a_1 \cos \frac{\alpha_1}{2}+2a_2 \cos \beta,a_1 \sin \frac{\alpha_1}{2})\nonumber\\ &A_4 = (a_1 \cos \frac{\alpha_1}{2}+2a_2 \cos \beta,-a_1 \sin \frac{\alpha_1}{2})\nonumber\\ \end{align} \]
由参考资料[1]中推得的结果有:
\[ t \sum_{n} a_{n}^\dagger b_{n} =t \sum_{k} a_{k}^\dagger b_{k} e^{i k\vec{r}}\tag{2} \]
其中\(\vec{r}\)是a到b的位置向量。所以对于\(A_1\)原子有
\[ \begin{align} t_1 \sum A_1^\dagger B &= t_1 \sum A_k^\dagger B_k e^{i [k_x(a_1 \cos \frac{\alpha_1}{2})+k_y(a_1 \sin \frac{\alpha_1}{2})]}\nonumber\\ &=t_1 \sum A_k^\dagger B_k e^{ik_x a_1 \cos \frac{\alpha_1}{2}} e^{ik_ya_1 \sin \frac{\alpha_1}{2}}\nonumber \end{align} \]
对于AB的两个最近邻项有
\[ \begin{align} &t_1 \sum (A_1^\dagger B +A_2^\dagger B) \nonumber\\ & = t_1 \sum A_k^\dagger B_k [e^{ik_x a_1 \cos \frac{\alpha_1}{2}} e^{ik_ya_1 \sin \frac{\alpha_1}{2}} + e^{ik_x a_1 \cos \frac{\alpha_1}{2}}e^{-ik_ya_1 \sin \frac{\alpha_1}{2}}]\nonumber\\ & =\sum A_k^\dagger B_k \left \{ 2t_1 \cos [k_ya_1\sin (\alpha_1/2)]\times exp[ik_x a_1 \cos (\alpha _1/2)] \right \}\nonumber \end{align} \]
另外两个次近邻项有
\[ \begin{align} &t_1 \sum (A_3^\dagger B +A_4^\dagger B) \nonumber\\ & =\sum A_k^\dagger B_k \left \{2 t_3 \cos [k_ya_1\sin (\alpha_1/2)]\times exp\{-ik_x [a_1 \cos (\alpha _1/2)+2a_2 \cos \beta ] \} \right \}\nonumber \end{align} \]
上两者大括号内部分只和即为原子AB间的跃迁项,记为
\[ \begin{aligned} t_{A B}(k)=& 2 t_{1} \cos \left[k_{y} a_{1} \sin \left(\alpha_{1} / 2\right)\right] \times \exp \left[i k_{x} a_{1} \cos \left(\alpha_{1} / 2\right)\right] \\ &+2 t_{3} \cos \left[k_{y} a_{1} \sin \left(\alpha_{1} / 2\right)\right] \times \exp \left\{-i k_{x}\left[a_{1} \cos \left(\alpha_{1} / 2\right)+2 a_{2} \cos \beta\right]\right\} \end{aligned}\tag{3} \]
同理可得CB,DB项
\[ t_{C B}(k)=t_{2} \exp \left[-i k_{x} a_{2} \cos \beta\right]+t_{5} \exp \left\{i k_{x}\left[2 a_{1} \cos \left(\alpha_{1} / 2\right)+a_{2} \cos \beta\right]\right\}\tag{4} \] \[ t_{D B}(k)=4 t_{4} \cos \left[k_{y} a_{1} \sin \left(\alpha_{1} / 2\right)\right] \cos \left\{k_{x}\left[a_{1} \cos \left(\alpha_{1} / 2\right)+a_{2} \cos \beta\right]\right\}\tag{5} \]
有了式(2)(3)(4)后我们可以看出一些没有写出表达式的如AC间跳跃,是可以等价于已写出的表达式BD间的跳跃的。
为此以ABCD四个原子的电子波函数作为本征态,写出单层黑磷的哈密顿量
\[ H_{\text {m}}=\left(\begin{array}{ll} H_{0} & H_{1} \\ H_{1} & H_{0} \end{array}\right)\tag{6} \]
其中 \[ \begin{array}{l} H_{0}=\left(\begin{array}{cc} 0 & t_{A B}(k) \\ t_{A B}^{*}(k) & 0 \end{array}\right) \\ H_{1}=\left(\begin{array}{cc} t_{D B}(k) & t_{C B}(k) \\ t_{C B}^{*}(k) & t_{D B}(k) \end{array}\right) \end{array} \]
2.使用python绘制能带图
先给出一个参数文件 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15# para.py
import numpy as np
# 黑磷晶格参数
a1 = 2.22
a2 = 2.24
alpha1 = np.pi*96.5/180
alpha2 = np.pi*101.9/180
cos_beta = -np.cos(alpha2)/np.cos(alpha1/2)
t1 = -1.220
t2 = 3.665
t3 = -0.205
t4 = -0.105
t5 = -0.055
给出单层黑磷的代码
1 | from para import * |
main1()是用来画一维的能带,main2()是画立体的。单层黑磷的能带结构图如下:
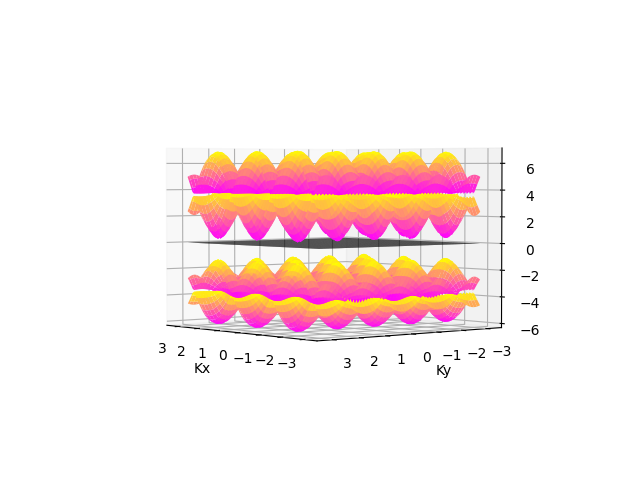
同时会输出带隙,在1.52左右,是符合之前的工作结果的。
4.参考资料
[2] 罗雪琴. 外电场相关不同层数黑磷双光子吸收性质的理论研究[D].云南师范大学,2021.DOI:10.27459/d.cnki.gynfc.2021.001019.
[3] 关济寰大佬的博客石墨烯哈密顿量与能带图(附Python代码)