能带理论-紧束缚近似与二次量子化表示

发表于 2022-04-28 更新于 2023-03-04 分类于学习笔记，物理本文字数： 4.1k 阅读时长 ≈ 4 分钟

摘要

紧束缚近似的二次量子化哈密顿量表示

1.近自由电子近似和紧束缚近似

对于固体这样的多粒子体系，严格求解每个粒子的运动在目前的算力下是不可能的。

为此物理学家必须通过近似来简化问题，如近自由电子近似，它忽略了电子和电子、电子和晶格离子之间的相互作用，并认为电子是独立和自由的。这样周期性势场的起伏就会比较小，进而先计算零级近似的稳定场，再将周期起伏当作微扰来处理。

这种近似方法对金属来说效果不错，因为金属本身最外层电子的运动就比较自由，但对于其他固体，甚至是对金属内部的电子，来说近自由电子近似不是很合理。

而紧束缚近似的出发点是晶体中的原子间距较大，电子受到原子实的紧紧束缚，电子的运动不受到其他势场的影响。所以电子的行为会和孤立原子中电子的行为相似，这也是紧束缚近似也被称为原子轨道线性组合(LCAO)法的原因。

近自由电子近似和紧束缚近似其实就是考虑了两种极端的近似。

近自由电子近似有着原子核扰动(perturbation)，紧束缚近似有着原子间的跃迁(hopping).所以都会产生禁带和导带。近自由电子近似使用的是布洛赫表象，紧束缚近似使用的是瓦尼尔表象。

定量计算绝缘体、化合物、半导体等能带方面，紧束缚近似使用会较多。

2.二次量子化

一次量子化是将物理量变为了算符。

但对于全同粒子体系，使用坐标表象来表达和计算还是相当繁琐。因为数量比较多了，要给粒子编号。

实际上我们并不关心每一个粒子的状态，要计算的是体系的状态，所以只需要标记出一单粒子态上有多少粒子数就足够了。

所以物理学家给量子力学打了个补丁叫二次量子化，引入了产生算符和湮灭算符。

\[ 产生算符: c^{\dagger}\\ 湮灭算符: c \]

对于产生和湮灭算符，他们也可在实空间和倒空间进行傅里叶级数展开：

\[ \begin{aligned} c_{r} &=\frac{1}{\sqrt{N}} \sum_{k} c_{k} e^{i k r} \\ c_{k} &=\frac{1}{\sqrt{N}} \sum_{r} c_{i} e^{-i k r} \end{aligned} \tag{1} \]

根据傅里叶级数基底的正交性，又有

\[ \begin{aligned} \frac{1}{N} \sum_{k} e^{i k r} e^{-i k r^{\prime}}=\delta_{r r^{\prime}} \\ \frac{1}{N} \sum_{r} e^{i k r} e^{-i k^{\prime} r}=\delta_{k k^{\prime}} \end{aligned} \tag{2} \]

3.紧束缚近似下的二次量子化方法表示晶体哈密顿量

晶体的哈密顿量通常由动能势能和晶格间的相互作用能表示，在紧束缚近似下，晶格间相互作用和动能统一考虑为运动项，即跳跃能（hopping），而势能项（在位能 on site energy）没有太大意义，单纯只是增加一个常数。所以可以将哈密顿量写成如下形式。

\[ H=\sum_{\langle i, j\rangle} t_{i j} c_{i}^{\dagger} c_{j} \tag{3} \]

其中i和j表示不同的晶格，t是跳变参数，<>表示近邻项,虽然远距离跃迁是可以的，但概率比较低，可以选择忽略。两个原子间的相互跃迁在数值上是共轭对，实际上写出一半即可。

下面用紧束缚模型下的二次量子化的方法来计算一下一维双原子链模型：

先写出哈密顿量的表达式

\[ H=-t \sum_{n}\left(a_{n}^\dagger b_{n} + b_{n}^\dagger a_{n+1} + h . c .\right)+V_{a} \sum_{n} a_{n}^\dagger a_{n}+V_{b} \sum_{n} b_{n}^\dagger b_{n}\tag{4} \]

第一项是动能项，电子在a，b位置间的跳跃，其中t是常数。后两项是在a或b点的势能，也是常数。h.c.是厄米共轭项。

现计算第一项：

\[ \begin{aligned} -t \sum_{n} a_{n}^\dagger b_{n} &=-t \frac{1}{N} \sum_{n}\left(\sum_{k} a_{k}^\dagger e^{-i k r_{a}}\right)\left(\sum_{k^{\prime}} b_{k^{\prime}} e^{i k^{\prime} r_{b}}\right) \\ &=-t \frac{1}{N} \sum_{n} \sum_{k} \sum_{k^{\prime}} a_{k}^\dagger b_{k^{\prime}} e^{-i k r_{a}} e^{i k^{\prime} r_a }e^{i k^{\prime}(r_b-r_a)}\\ &=-t \sum_{k} \sum_{k^{\prime}} a_{k}^\dagger b_{k^{\prime}} e^{ik^{\prime} (r_{b}-r_{a})} \delta_{k k^{\prime}} \\ &=-t \sum_{k} a_{k}^\dagger b_{k} e^{i k\left(r_{b}-r_{a}\right)} \end{aligned}\tag{5} \]

同理可得 \[ -t \sum_{n} b_{n}^\dagger a_{n+1} = -t \sum_{k} b_{k}^\dagger a_{k} e^{i k\left(r_{a}-r_{b}\right)}\tag{6} \]

假设晶格常数为a，则其中\(r_b-r_a = \frac{a}{2}\)

对势能项有：

\[ \begin{aligned} \sum_{n} a_{n}^\dagger a_{n} &=\frac{1}{N}\sum_{n}\left(\sum_{k} a_{k}^\dagger e^{-i k r_{a}}\right)\left(\sum_{k^{\prime}} a_{k^{\prime}} e^{i k^{\prime} r_{a}}\right) \\ &=\frac{1}{N}\sum_{n} \sum_{k} \sum_{k^{\prime}} a_{k}^\dagger a_{k^{\prime}} e^{i r_{a}\left(k^{\prime}-k\right)} \\ &=\sum_{k} a_{k}^\dagger a_{k} \end{aligned}\tag{7} \]

将所有项代入式(4)

\[ \begin{aligned} H &=-t \sum_{n}\left(a_{n}^\dagger b_{n}+b_{n}^\dagger a_{n+1}+h . c .\right)+V_{a} \sum_{n} a_{n}^\dagger a_{n}+V_{b} \sum_{n} b_{n}^\dagger b_{n} \\ &=\sum_{k}\left(\left(-2 t \cos \left(\frac{k a}{2}\right)\right) a_{k}^\dagger b_{k}+\left(-2 t \cos \left(\frac{k a}{2}\right)\right) b_{k}^\dagger a_{k}+V_{a} a_{k}^\dagger a_{k}+V_{b} b_{k}^\dagger b_{k}\right) \\ &=\sum_{k}\left[a_{k}^\dagger b_{k}^\dagger\right]\left[\begin{array}{cc} V_{a} & -2 t \cos \left(\frac{k a}{2}\right) \\ -2 t \cos \left(\frac{k a}{2}\right) & V_{b} \end{array}\right]\left[\begin{array}{l} a_{k} \\ b_{k} \end{array}\right] \end{aligned}\tag{8} \]

其中 \[ \left[\begin{array}{cc} V_{a} & -2 t \cos \left(\frac{k a}{2}\right) \\ -2 t \cos \left(\frac{k a}{2}\right) & V_{b} \end{array}\right]\tag{9} \]

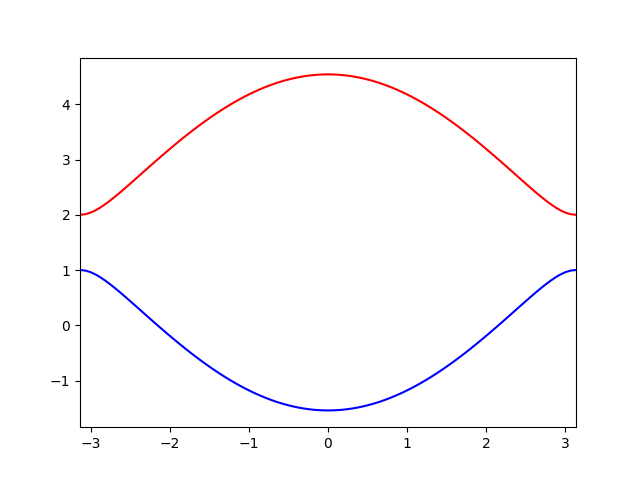
即为一维双原子链的哈密顿量的核，该矩阵的大小由选取的量子态数量决定，该矩阵的特征值求出该矩阵的特征值就可以得到一维双原子链的色散关系。

使用python求出矩阵的特征值并绘制色散曲线如下：

import numpy as np
import matplotlib.pyplot as plt

def h(k):
    h0 = np.zeros((2, 2), dtype=complex)

    h0[0,0] = 1
    h0[1,1] = 2
   
    h0[0,1] = -2*t*np.cos(k/2)
    h0[1,0] = h0[0,1]

    return h0

t = 1.5
la = 1
n_step = 100
k = np.linspace(-np.pi/la, np.pi/la, n_step)
eig = np.zeros((n_step, 2))
for x in range(n_step):
    kx = k[x]
    ham = h(kx)
    eig[x,:], vet = np.linalg.eigh(ham)


plt.plot(k, eig[:,0], '-b')
plt.plot(k, eig[:,1], '-r')
plt.xlim([-np.pi/la, np.pi/la])
plt.show()