机器学习实战1

发表于 更新于 分类于 ， 本文字数： 12k 阅读时长 ≈ 11 分钟

摘要

《机器学习实战：基于Scikit-Learn和TensorFlow》学习笔记

加州房价

1.机器学习概览

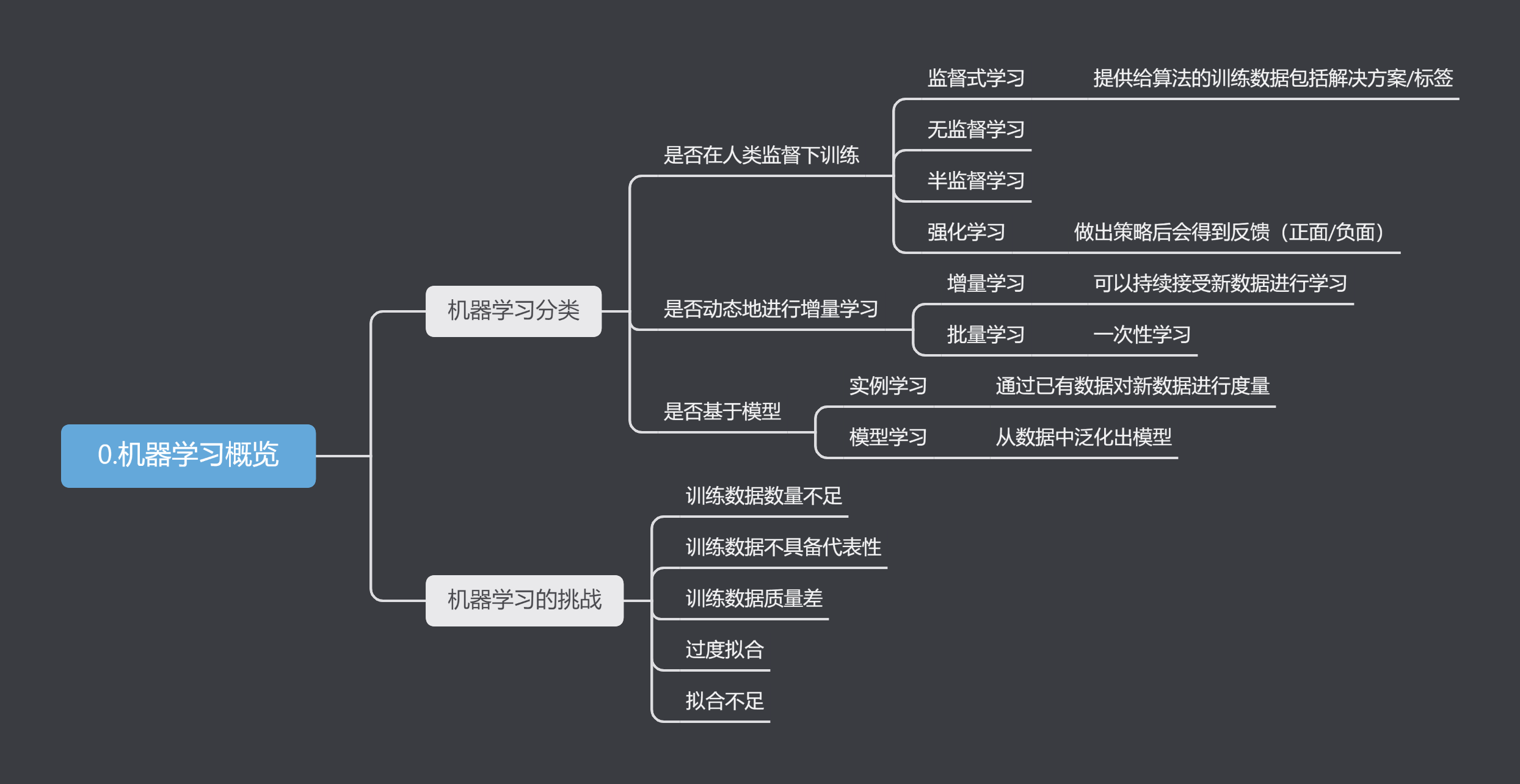
机器学习概览

2.机器学习项目--加州房价预测

假设你是一个房地产公司最近新雇佣的数据科学家，你需要根据加州房价数据集建立一个房价模型，使其能预测任意区域的房价中位数。

以下是你可能需要经历的步骤流程

  1. 观察大局
  2. 获得数据
  3. 从数据探索和可视化中获得洞见
  4. 机器学习算法的数据准备
  5. 选择和训练模型
  6. 微调模型
  7. 展示解决方案
  8. 启动、监控和维护系统

2.1 观察大局

首先我们需要明确目标，输入和输出是什么？数据是否包含结果？数据是否会更新？

这些问题会决定你的机器学习模型应该是什么样的。输入是人口收入中位数等信息，显然这应该设定为监督式学习，房价数据肯定会更新，但变化不快，批量学习也能接受。

对于房价预测问题，有接触过机器学习的应该都能看出这就是一个典型的多元回归任务。

接下来应该选取一个合适的性能指标，回归问题的典型衡量指标是均方根误差（RMSE），计算公式如下

\[ RMSE(\mathbf{X},h) = \sqrt[]{\frac{1}{m}\sum_{i=1}^{m}(h(\mathbf{x}^{\left ( i \right ) })-y^{(i)} )^2 } \]

其中h()是预测函数，\(\mathbf{x}^{(i)}\)是指数据集中第i个实例的所有特征值向量。\(y^{(i)}\)是标签值。

所以\(h(\mathbf{x}^{\left ( i \right ) })\)是预测值，它和标签值的差的平方可以被当作偏离误差。也是机器学习中常用的标准。如果不开根号就叫做均方根误差（MSE）

另一个常用的是平均绝对误差（MAE）公式如下：

\[ MAE(\mathbf{X},h) = \frac{1}{m}\sum_{i=1}^{m}\left | (h(\mathbf{x}^{\left ( i \right ) })-y^{(i)} ) \right | \]

2.2 获取数据

数据文件点击下载

我这里直接用的jupyter

使用pandas库加载数据，使用head()方法快速参看前5行。

1
2
3
4
5
6
7
import pandas as pd
def loading_housing_data():
    csv_data = pd.read_csv(r'datasets\housing\housing.csv')
    return csv_data

housing = loading_housing_data()
housing.head()
查看数据

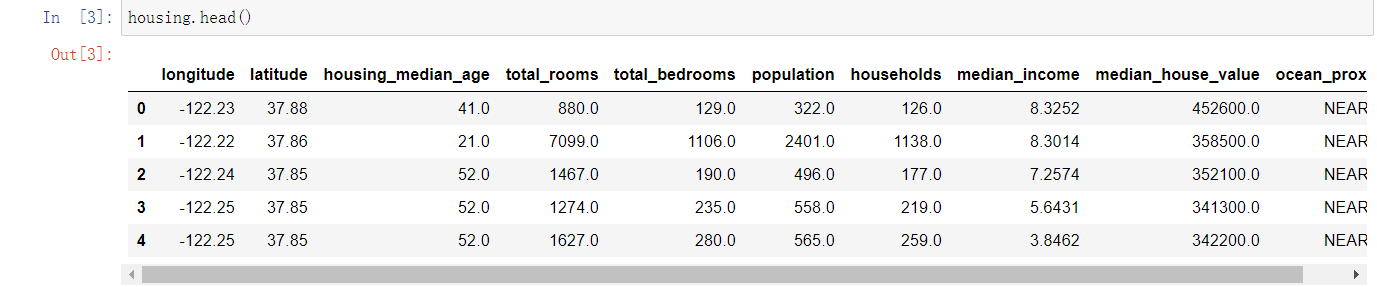
可以看出数据共有10个属性，使用info()方法可以查看属性类型及数量,describe()方法可以显示属性值摘要。

使用value_counts()方法可以查看该列又多少种分类。 

1
2
3
4
5
6
7
8
>>>housing['ocean_proximity'].value_counts()
output:
<1H OCEAN     9136
INLAND        6551
NEAR OCEAN    2658
NEAR BAY      2290
ISLAND           5
Name: ocean_proximity, dtype: int64

使用matplotlib库可以快速绘制直方图 

1
2
3
import matplotlib.pyplot as plt
housing.hist(bins = 50,figsize=(20,15))
plt.show()
bin是指每张图的柱子个数，figsize是图片大小。

快速查看数据的方法

1
2
3
4
5
housing.head() # 前5行
housing.info() # 查看属性类型及数量
housing.describe() # 显示属性值摘要
housing['ocean_proximity'].value_counts() # 查看分类
housing.hist(bins = 50,figsize=(20,15)) # 绘制直方图

在浏览完数据后，就需要划分训练集和测试集。在数量庞大的情况下可以选择随机划分，为保证每次运行的训练集和测试集相同，最好是分完就保存或者设定一个随机数种子。

另一个方法是更具标识符来划分，这样新增的数据可以通过打标识来解决，而前面的不需要变化。常用的标识符是哈希值。

以上讨论的都是随机划分，但有时候这样做选出来的数据不够典型。以房价为例，房价和人居收入必然是紧密联系的，我们应当在各个收入阶层都选出按照原数据比例选出。

为此我们不妨新增一个属性，起名叫“income_cat”，将人群按收入高低划分为5类 

1
2
3
import numpy as np
housing["income_cat"] = np.ceil(housing["median_income"]/1.5)
housing["income_cat"].where(housing["income_cat"]<5,5.0,inplace=True)
现在使用Scikit-learn的StratifiedShuffle Split类进行分层抽样。

使用Split类进行分层抽样

1
2
3
4
5
6
7
from sklearn.model_selection import StratifiedShuffleSplit

split = StratifiedShuffleSplit(n_splits=1,test_size=0.2,random_state=42)
for train_index,test_index in split.split(housing,housing["income_cat"]):
    strat_train_set = housing.loc[train_index]
    strat_test_set = housing.loc[test_index]

参数n_splits 是将训练数据分成train/test对的组数。

参数test_size和train_size是用来设置train/test对中train和test所占的比例。

参数random_state控制随机。

使用下面命令查看是否根据收入比例分配 

1
2
housing["income_cat"].value_counts()/len(housing)
strat_train_set["income_cat"].value_counts()/len(strat_train_set)
完成后删去"income_cat"恢复原始数据 
1
2
for set in (strat_train_set,strat_test_set):
    set.drop(["income_cat"],axis=1,inplace=True)

2.3 从数据探索和可视化中获得洞见

分配好训练集和测试集后，我们需要对数据有更深入的洞察，先创建一个训练集副本 

1
housing = strat_train_set.copy()
在房价问题中，不妨先用热力图看下地图信息 
1
2
3
4
5
housing.plot(kind="scatter",x="longitude",y="latitude",alpha=0.4,
            s=housing["population"]/100,label="population",
            c="median_house_value",cmap=plt.get_cmap("jet"),colorbar=True,
            )
plt.legend()
上面参数s指size，c指color，cmap是配色方案。

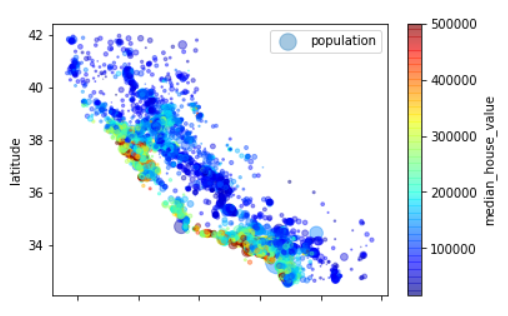
高密度区域可视化

可以看出，靠近西海岸的房价会比较高。

由于数据集不大，可以使用corr()方法计算出属性间的相关性 

1
2
3
4
5
6
7
8
9
10
11
12
13
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
coutput:
median_house_value    1.000000
median_income         0.687151
total_rooms           0.135140
housing_median_age    0.114146
households            0.064590
total_bedrooms        0.047781
population           -0.026882
longitude            -0.047466
latitude             -0.142673
Name: median_house_value, dtype: float64
相关系数是-1到1之间的值，越接近1说明有越强的正相关性；越接近-1有越强的负相关性；越接近0说明越不相关。

试验不同属性的组合。在获得数据的相关性后，我们也可以自行构建数据，比如“房间总数”没什么用，但它除以“家庭户数”就可以得到平均一家有多少房间，同样“卧室总数”也可以这么处理。

1
2
3
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"] = housing["population"]/housing["households"]

再处理完后可以再参看一次相关性 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
output:
median_house_value          1.000000
median_income               0.687151
rooms_per_household         0.146255
total_rooms                 0.135140
housing_median_age          0.114146
households                  0.064590
total_bedrooms              0.047781
population_per_household   -0.021991
population                 -0.026882
longitude                  -0.047466
latitude                   -0.142673
bedrooms_per_room          -0.259952
Name: median_house_value, dtype: float64

看起来结果还可以，到了这一步我希望能将我的工作保存一下，当后面对数据进行一些处理后，我还能把这个自己组合出来的数据算出来。为此我应该建立一个函数或者是类。恰好scikit-learn已经提供了一些基础类型，只需要调用TransformerMixin和BaseEstimator作为基类，然后创建fit和transform方法。就可以将这一过程变为自定义转换器。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from sklearn.base import BaseEstimator,TransformerMixin
rooms_ix,bedrooms_ix,population_ix,household_ix = 3,4,5,6
class CombinedAttributesAdder(BaseEstimator,TransformerMixin):
    def __init__(self, add_bedrooms_per_room = True):#no *args or **kargs
        self.add_bedrooms_per_room = add_bedrooms_per_room
    def fit(self, X, y=None):
        return self  # nothing else to do
    def transform(self, X, y=None):
        rooms_per_household = X[:, rooms_ix] / X[:, household_ix]
        population_per_household = X[:, population_ix] / X[:, household_ix]
        if self.add_bedrooms_per_room:
            bedrooms_per_room = X[:, bedrooms_ix] / X[:, rooms_ix]
            return np.c_[X, rooms_per_household, population_per_household,
                         bedrooms_per_room]
        else:
            return np.c_[X, rooms_per_household, population_per_household]

其中np.c_是按列合并array

2.4 机器学习算法的数据准备

这一步需要我们对数据开始正式处理，前面的都只是在观察，先回到一个干净的数据集,drop()方法会创建一个副本，不会影响到训练集。 

1
2
housing = strat_train_set.drop("median_house_value",axis=1)
housing_labels = strat_train_set["median_house_value"].copy()

2.4.1 数值处理

下一步就是数据清理，因为有限属性存在部分数据缺失，解决方法有三种 1. 放弃该行数据 2. 放弃该列数据 3. 补全该数据

放弃改行可以使用housing.dropna(subset=["total_bedrooms"])

放弃该列可以使用housing.drop("toatl_bedrooms",axis=1)

补全可以使用中位数、平均值、或直接用0进行补全 housing["total_bedrooms"].fillna(median)

对于补全scikit-learn还提供了imputer类来辅助处理。 这里版本问题，代码和书上略有不同 

1
2
3
4
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy="median")
housing_num = housing.drop("ocean_proximity",axis=1) # 把文本属性的先去除
imputer.fit(housing_num) # 计算出所有拟补全数据
可以使用imputer.statistics_参看各列的拟补全数据。

现在可以补全数据并加回文本属性数据 

1
2
X = imputer.transform(housing_num)
housing_tr = pd.DataFrame(X,columns=housing_num.columns)

2.4.2 文本处理

现在完成了数据的补全，但对于文本信息我们还没进行处理，计算机对于数字更敏感，所以我们最好把文本信息转换为数字。

scikit-learn中的LabelEncoder刚好可以处理这个问题： 

1
2
3
4
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
housing_cat = housing["ocean_proximity"]
housing_cat_encoded = encoder.fit_transform(housing_cat)

使用encoder.classes_查看映射

但这种直接的编码方法不是很好，比如海岛和近海的属性比较像，但数值却一个为0一个为4，为解决这个方法，我们可以使用OneHotEncoder进行独热编码，

1
2
3
4
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder()
housing_cat_1hot = encoder.fit_transform(housing_cat_encoded.reshape(-1,1))
housing_cat_1hot

reshape(-1,1)中的-1指未设定行数，程序自动分配。

使用LabelBinarizer可以直接一步到位 

1
2
3
4
from sklearn.preprocessing import LabelBinarizer
encoder = LabelBinarizer(sparse_output=True)
housing_cat_1hot= encoder.fit_transform(housing_cat)
housing_cat_1hot

清洗好数据之后，我们可以利用之前编写的类将自定义的属性添加进来。

2.4.3 特征缩放

特征缩放也是数据处理中的重要一环，如果有部分数据数值过大，很有可能会影响到结果，最好是参数范围差不多。

常用缩放方法有两种： 1. 最小-最大放缩

这种方法又称为归一化，是将数据映射为0-1之间。实现方法是（目标值-最小值）/（最大值-最小值）

  1. 标准化

    标准化的均值总是为0，计算方法是（m-mean）/方差，它受异常值的影响会笔记小。

2.4.4 转换流水线

在数据清洗和处理的过程都是按照一个顺序进行的，很像工厂里的流水线，scikit-learn正好提供了Pipeline来支持这样的处理。

1
2
3
4
5
6
7
8
9
10
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
 
num_pipeline = Pipeline([
        ('imputer', SimpleImputer(strategy="median")),
        ('attribs_adder', CombinedAttributesAdder()),
        ('std_scaler', StandardScaler()),#标准化转换器
    ])
 
housing_num_tr = num_pipeline.fit_transform(housing_num)

这时候不妨回头看一下这些过程，第一个是补全，使用的SimpleImputer类，第二个是自定义的CombinedAttributesAdder类，第三个是标准化缩放类StandardScaler

它们都被要求有fit_transform()方法。考虑到scikit-learn不支持DataFrame，为此我们可能会需要用到一个df转ndarray的类。

1
2
3
4
5
6
7
8
9
from sklearn.base import BaseEstimator, TransformerMixin

class DataFrameSelector(BaseEstimator, TransformerMixin):
    def __init__(self, attribute_names):
        self.attribute_names=attribute_names
    def fit(self, X, y=None):
        return self
    def transform(self, X):
        return X[self.attribute_names].values

然后把处理文本的流水线也加进来，额外的使用一个ColumnTransformer类来并行处理这些数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from sklearn.compose import ColumnTransformer


num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]

num_pipeline = Pipeline([
    ('selector',DataFrameSelector(num_attribs)),
    ('imputer', SimpleImputer(strategy="median")),
    ('attribs_adder', CombinedAttributesAdder()),
    ('std_scaler', StandardScaler()),#标准化转换器
])

cat_pipeline = Pipeline([
    ('selector',DataFrameSelector(cat_attribs)),
    ('label_binarizer',LabelBinarizer()),
])

full_pipeline = ColumnTransformer([
        ("num", num_pipeline, num_attribs),
        ("cat", OneHotEncoder(), cat_attribs),
    ])
 
housing_prepared = full_pipeline.fit_transform(housing)

2.5 选择和训练模型

2.5.1 建立模型

目前我们已经可以自动化洗数据了，接下来我们应该整一个回归模型！

先来个线性回归看看 

1
2
3
4
from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)
训练好了，使用均方根误差看看效果

1
2
3
4
5
6
7
8
from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse=np.sqrt(lin_mse)
lin_rmse

output:
68627.87390018745

emmm,貌似效果不太行，要不换成决策树？ 

1
2
3
4
5
6
7
8
9
10
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor()
tree_reg.fit(housing_prepared, housing_labels)
housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse

output:
0.0
emmm,没有误差也太假了，看来是过拟合了。

2.5.2 交叉验证

注意，这时候我们还没有动测试集，我们也不应该动。评估决策树模型还可以使用交叉验证，以下是k-折交叉验证的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from sklearn.model_selection import cross_val_score
scores = cross_val_score(tree_reg, housing_prepared, housing_labels, scoring = 'neg_mean_squared_error',cv=10)
tree_rmse_scores = np.sqrt(-scores)

def display_scrores(scores):
    print("scores:",scores)
    print("Mean:",scores.mean())
    print("standard dviation:",scores.std())

display_scrores(tree_rmse_scores)

output:
scores: [73138.67517572 71506.36370902 68525.17513869 71289.0410928
 68730.16014932 78124.19174839 70826.82238157 75178.21352962
 68631.28499359 70483.13744005]
Mean: 71643.30653587906
standard dviation: 2935.505119383448

和线性回归做个对比

1
2
3
4
5
6
7
8
9
10
11
lin_scores = cross_val_score(lin_reg,housing_prepared,housing_labels,scoring='neg_mean_squared_error',cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)

display_scrores(lin_rmse_scores)

output:
scores: [71762.76364394 64114.99166359 67771.17124356 68635.19072082
 66846.14089488 72528.03725385 73997.08050233 68802.33629334
 66443.28836884 70139.79923956]
Mean: 69104.07998247063
standard dviation: 2880.3282098180666

两者半斤八两。

再来试试随机森林 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor()

forest_reg.fit(housing_prepared, housing_labels)
housing_predictions = forest_reg.predict(housing_prepared)
forest_rmse = np.sqrt(mean_squared_error(housing_labels, housing_predictions))
forest_rmse

forest_rmse_scores = cross_val_score(forest_reg,housing_prepared,housing_labels,scoring='neg_mean_squared_error',cv=10)
forest_rmse_scores = np.sqrt(-forest_rmse_scores)
display_scrores(forest_rmse_scores)

output:
scores: [51437.73602527 49070.23768941 46719.25099192 52092.63291424
 47390.46029858 51348.37861955 52067.85418266 49650.99947482
 48476.17361121 54240.18337563]
Mean: 50249.39071832983
standard dviation: 2253.416487488719

略好一筹。

2.5.2 保存模型

尝试过的模型应该好好保存，因为你永远不知道哪个模型是最好的。记得还得保存一下训练参数，joblib就用来是保存的库

1
2
3
4
5
import joblib

joblib.dump(forest_reg,"随机森林.pkl") # 保存

my_model_loaded = joblib.load("随机森林.pkl") # 读取

2.6 微调模型

微调的一种方法是网格搜索，它会尝试多个超参数的值来找到最佳的组合，这里简单看一下即可。

1
2
3
4
5
6
7
8
from sklearn.model_selection import GridSearchCV
param_grid = [
    {'n_estimators':[3,10,30], 'max_features':[2,4,6,8]},
    {'bootstrap':[False],'n_estimators':[3,10],'max_features':[2,3,4]},
]
forest_reg = RandomForestRegressor()
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,scoring='neg_mean_squared_error')
grid_search.fit(housing_prepared, housing_labels)

neg_mean_squared_error 是负均方根