谱线展宽和线型函数
摘要
1.谱线展宽
理想情况下,无论是激光的出射光还是光谱的峰,在谱线上都应该是一条直线,由于各种因素的影响,其现实效果并非如此,而是会呈现出分布在中心频率附近的一个很小的频率范围内的线型。这就是谱线展宽,常见的谱线又可以分为均匀加宽和非均匀加宽(判别依据是能否分辨加宽源自哪一个原子)。
1.1 均匀加宽
自然加宽
受激原子在激发态上具有有限的寿命。会自发向低能级跃迁,导致谱线加宽,线型为洛伦兹线型。
碰撞加宽
大量原子(分子、离子)之间无规则“碰撞”引起的谱线加宽,线型为洛伦兹线型。
晶格振动加宽
激光器工作物质因晶格场的影响导致的谱线加宽。温度越高,振动越剧烈,谱线越宽。
1.2 非均匀加宽
多普勒加宽
多普勒加宽是由于作热运动的发光原子(分子)所发出的辐射的多普勒频移引起的。属于高斯线型。
晶格缺陷加宽
激光器如果使用的是固体工作物质,其不存在多普勒加宽,但因为晶格错位或空位等不均匀性也会产生非均匀加宽。
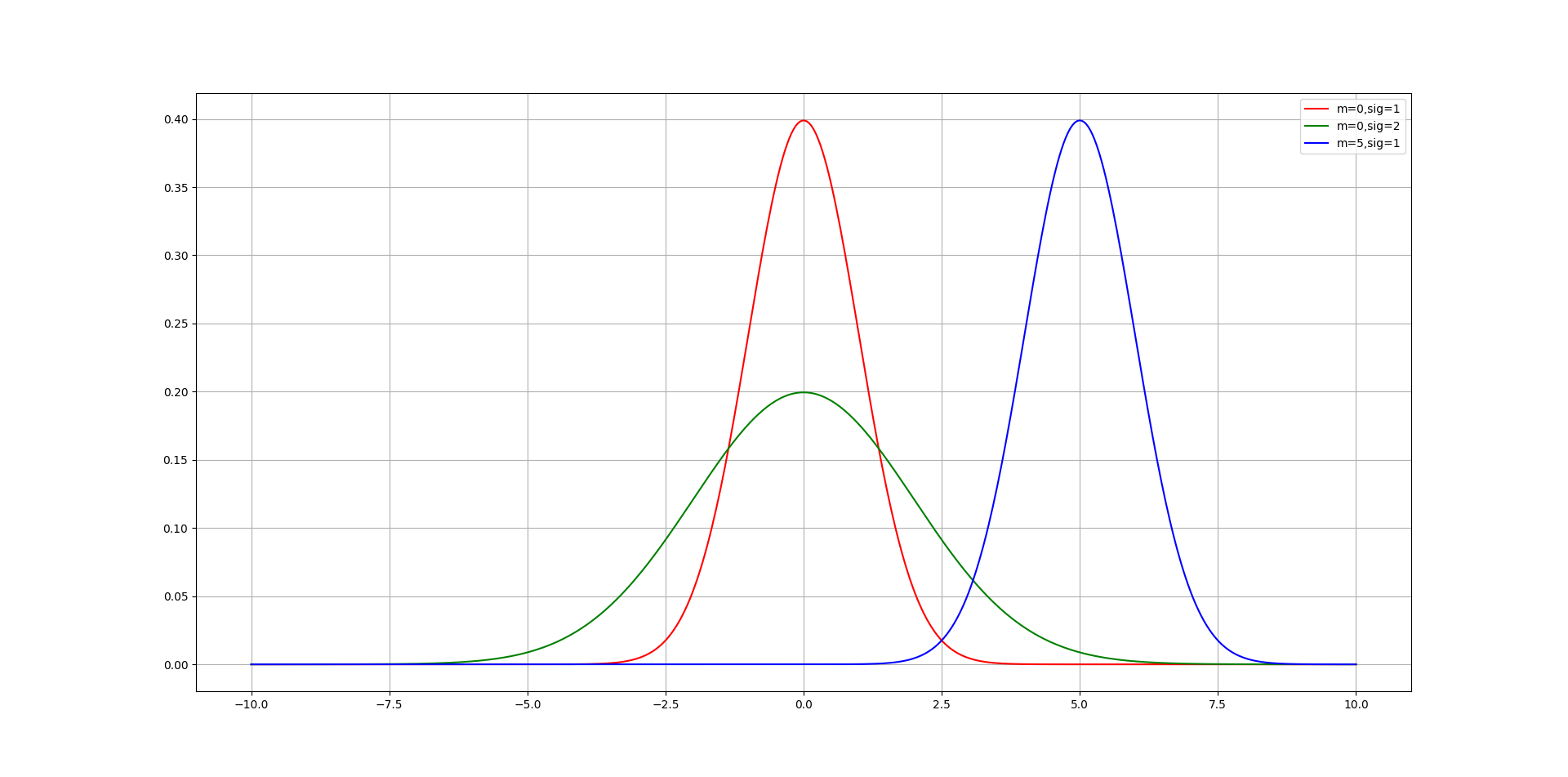
2.高斯线型
激光发射谱通常可以使用高斯线型拟合
一维高斯函数的公式如下: \[ G(x) = \frac{A}{\sigma \sqrt{2\pi}} \exp(-\frac{(x-x_c)^2 }{2\sigma ^2}) \]
和概率论中的正态分布一致,但是在origin的拟合中,origin是科研常用的画图软件,使用的是如下公式
1
2
3
4
5# y=y0 + (A/(w*sqrt(pi/2)))*exp(-2*((x-xc)/w)^2)
def Gauss_origin(x,y0,A,xc,w):
y = y0 + A * np.exp(-2*((x-xc)/w)**2)
return y
使用python画个图 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27import numpy as np
import matplotlib.pyplot as plt
def Gauss(x,A,xc,sigma):
y = A/(sigma*np.sqrt(2*np.pi))*np.exp(-(x-xc)**2/(2*sigma**2))
return y
mean1, sigma1 = 0, 1
x1 = np.linspace(-10, 10, 500)
mean2, sigma2 = 0, 2
x2 = np.linspace(-10, 10, 500)
mean3, sigma3 = 5, 1
x3 = np.linspace(-10, 10, 500)
y1 = Gauss(x1,1, mean1, sigma1)
y2 = Gauss(x2,1, mean2, sigma2)
y3 = Gauss(x3,1, mean3, sigma3)
plt.plot(x1, y1, 'r', label='m=0,sig=1')
plt.plot(x2, y2, 'g', label='m=0,sig=2')
plt.plot(x3, y3, 'b', label='m=5,sig=1')
plt.legend()
plt.grid()
plt.show()
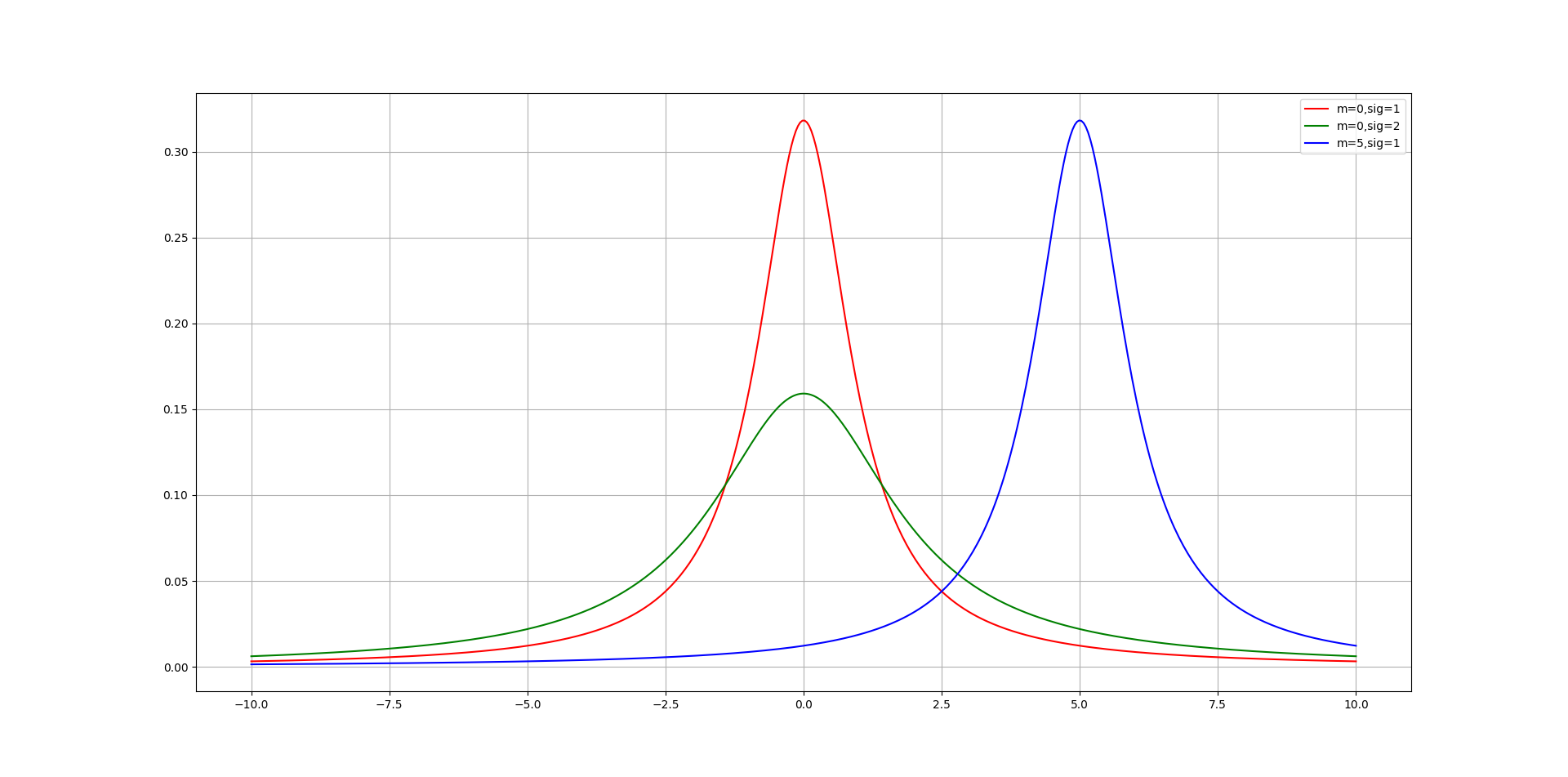
3.洛伦兹线型
与高斯线型比起来,洛伦兹线型显得更“瘦”
物质的光谱可以使用洛伦兹线型拟合
公式: \[ L(x) = \frac{A}{\pi} \frac{\sigma}{(x-x_c)^2 + \sigma^2} \]
在origin中使用公式
1 | # y = y0 + (2*A/pi)*(w/(4*(x-xc)^2 + w^2)) |
代码同上,修改两处即可 1
2
3
4
5
6
7
8def Lorentz(x,A,xc,sigma):
y = (A/np.pi)*(sigma/((x-xc)**2 + sigma**2))
return y
y1 = Lorentz(x1,1, mean1, sigma1)
y2 = Lorentz(x2,1, mean2, sigma2)
y3 = Lorentz(x3,1, mean3, sigma3)
4.voigt线型
其实上述线型还是有些理想化了,因为现实中往往是多个因素共同导致的谱线展宽,所以voigt线型才是最常用的,它是高斯线型和洛伦兹线型的卷积。
可以在Origin中查到voigt线型的公式
1 | // Mathematical expression is: |
python中numpy也有计算卷积的函数,但通常使用下面这个公式
1 | from scipy.special import wofz |
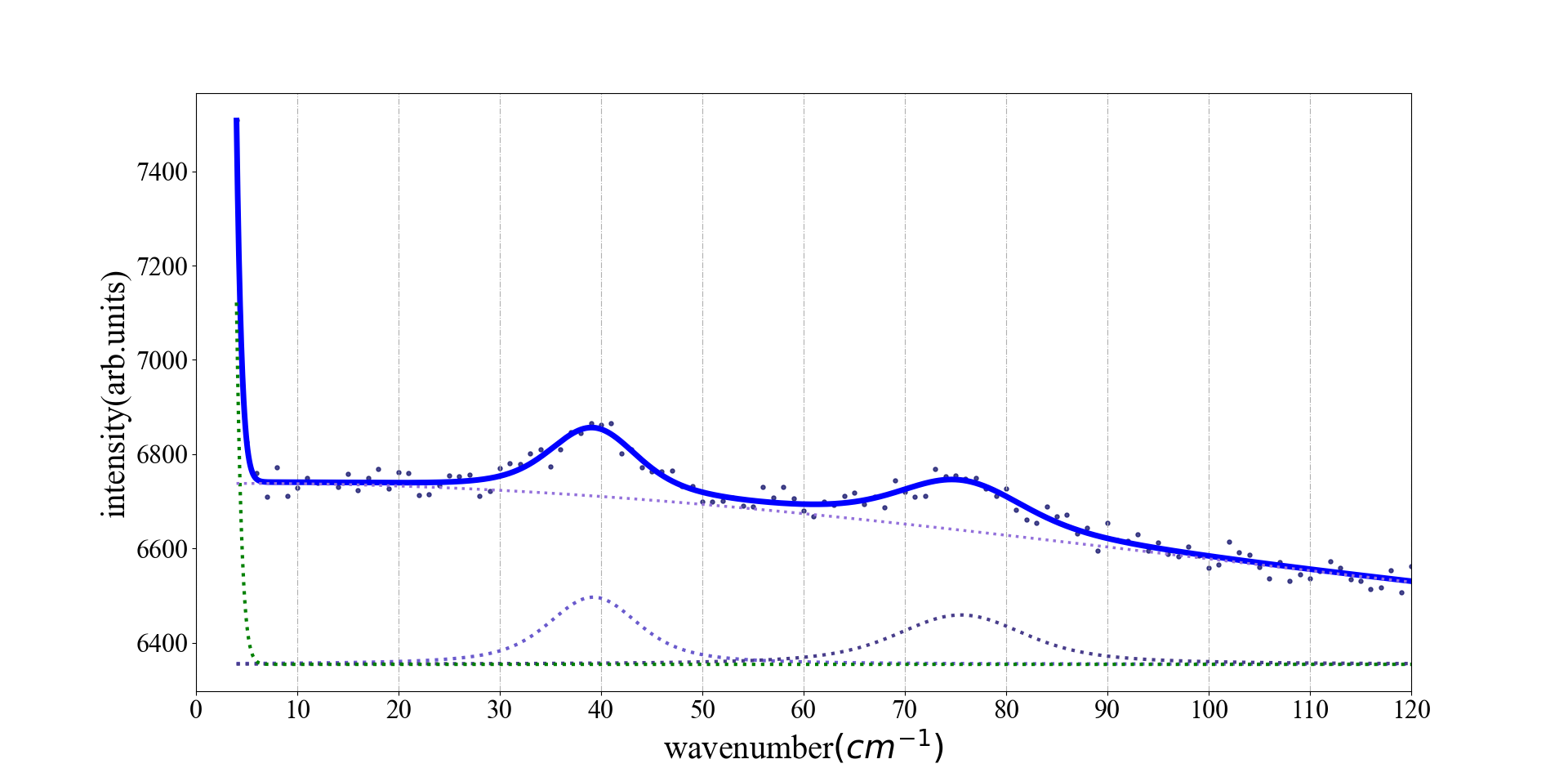
5.使用python进行拟合
对python绘图不太了解的可以参考使用python进行科研绘图
以我的实验数据为例,使用两个高斯峰和两个voigt拟合2层黑磷的超低频拉曼光谱。
其中一个高斯峰拟合瑞利散射的峰,一个高斯峰用来拟合基线。两个voigt峰分别拟合少层黑磷的CCM模和CH1模。
先看看实验数据 1
2
3
4
5
6
7
8
9
10
11
12
13
14import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
if __name__=='__main__':
df = pd.read_csv('筛选后的数据.csv')
x = df['w']
name = '2L'
layer = df[name]
x = x.values
layer = layer.values
plt.scatter(x, layer, alpha=0.8,s=13,color='midnightblue')
plt.show()
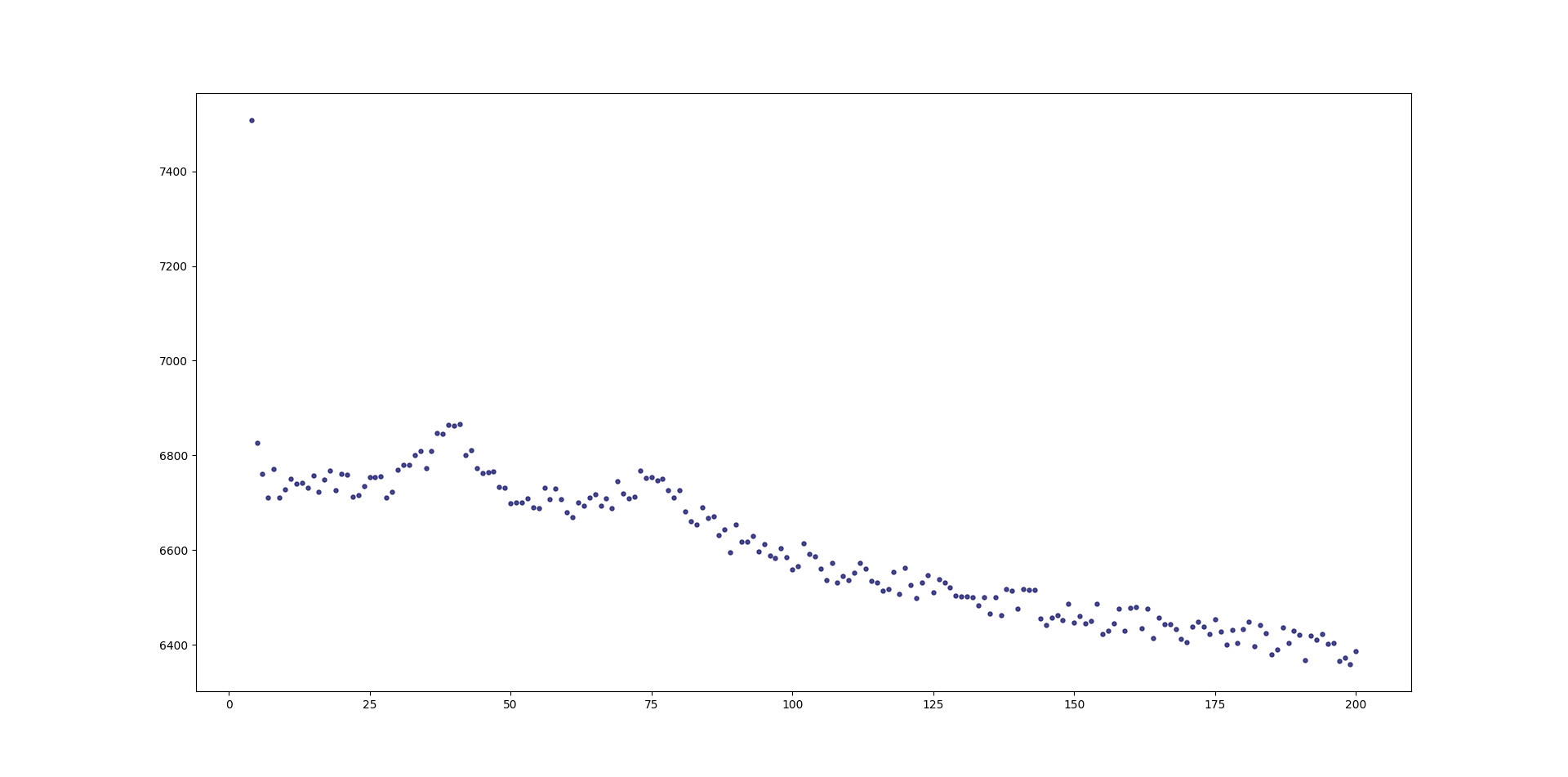
丑了点,加下面函数修饰一下,然后把上面最后一行改成ready_to_show()
1 | from matplotlib.pyplot import MultipleLocator |
放入拟合线型函数
1 | from scipy.special import wofz |
然后使用scipy.optimize中的curve_fit进行拟合
curve_fit
调用方式curve_fit(拟合曲线,x数据,y数据,p0 = 初始值,bounds = ([min1,min2...],[max1,max2...]))
然后拟合程序和显示都封装成函数,为了方便展示,我都放在同一个文件里,展示如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from scipy.special import wofz
from matplotlib.pyplot import MultipleLocator
def Gauss(x,y0,A,xc,w):
y = y0 + A * np.exp(-2*((x-xc)/w)**2)
return y
def Voigt(x, y0, amp, pos, fwhm, shape = 1):
tmp = 1/wofz(np.zeros((len(x))) + 1j*np.sqrt(np.log(2.0))*shape).real
return y0+tmp*amp*wofz(2*np.sqrt(np.log(2.0))*(x-pos)/fwhm+1j*np.sqrt(np.log(2.0))*shape).real
def my_fit_cure(x,y01,a1,p1,f1,y02,a2,p2,f2,y03,a3,xc3,w3,y04,a4,xc4,w4):
return Voigt(x,y01,a1,p1,f1)+Voigt(x,y02,a2,p2,f2)+Gauss(x,y03,a3,xc3,w3)+Gauss(x,y04,a4,xc4,w4)
def plot_scatter(x,st):
plt.scatter(x, st, alpha=0.8,s=13,color='midnightblue')
def show_the_fen(popt):
y01,a1,p1,f1,y02,a2,p2,f2,y03,a3,xc3,w3,y04,a4,xc4,w4 = popt
form = "{:10}\t{:10}\t{:10}\t{:10}\t{:10}"
print(form.format("峰类型","偏置","幅值","中心位置","宽度"))
print(form.format("voigt","%.2f"%y01,"%.2f"%a1,"%.2f"%p1,"%.2f"%f1))
print(form.format("voigt","%.2f"%y02,"%.2f"%a2,"%.2f"%p2,"%.2f"%f2))
print(form.format("gauss","%.2f"%y03,"%.2f"%a3,"%.2f"%xc3,"%.2f"%w3))
print(form.format("gauss","%.2f"%y04,"%.2f"%a4,"%.2f"%xc4,"%.2f"%w4))
def show_the_cure(xfit,popt,offset=0,cr='b'):
y01,a1,p1,f1,y02,a2,p2,f2,y03,a3,xc3,w3,y04,a4,xc4,w4 = popt
# 主线
yfit = my_fit_cure(xfit,y01,a1,p1,f1,y02,a2,p2,f2,y03,a3,xc3,w3,y04,a4,xc4,w4)
plt.plot(xfit,yfit+offset,linewidth=5.0,color = cr)
# 分峰
y00 = y01 + y02 + y03 + y04 + offset
# voigt
yfit1 = Voigt(xfit,y00,a1,p1,f1)
plt.plot(xfit,yfit1,linewidth=3.0,linestyle=':', color='slateblue')
yfit2 = Voigt(xfit,y00,a2,p2,f2)
plt.plot(xfit,yfit2,linewidth=3.0,linestyle=':', color='darkslateblue')
# gauss
yfit3 = Gauss(xfit,y00,a3,xc3,w3)
plt.plot(xfit,yfit3,linewidth=3.0,linestyle=':', color='g')
yfit4 = Gauss(xfit,y00,a4,xc4,w4)
plt.plot(xfit,yfit4,linewidth=2.5,linestyle=':', color='mediumpurple')
def plot_nihe(xx,popt,func):
xfit = np.linspace(xx.min(),xx.max(),5000)
if func == 'Lorentz':
yfit = Lorentz(xfit,popt[0],popt[1],popt[2],popt[3])
plt.plot(xfit,yfit,linewidth=5.0,color = 'r')
elif func == 'Gauss':
yfit = Gauss(xfit,popt[0],popt[1],popt[2],popt[3])
plt.plot(xfit,yfit,linewidth=5.0,color = 'r')
elif func == 'Vogit':
y0,amp, pos, fwhm = popt
yfit = Voigt(xfit, y0, amp, pos, fwhm)
plt.plot(xfit,yfit,linewidth=5.0,color = 'r')
elif func == 'my_fit_cure':
show_the_cure(xfit,popt)#展示拟合参数
show_the_fen(popt)#展示峰值曲线
def ready_to_show():
x_major_locator=MultipleLocator(10)#准备刻度
#标签
plt.xlabel('wavenumber$(\mathit{ cm^{-1}})$',fontdict={'family' : 'Times New Roman', 'size' : 29})
plt.ylabel('intensity(arb.units)',fontdict={'family' : 'Times New Roman', 'size' : 29})
ax=plt.gca()
ax.xaxis.set_major_locator(x_major_locator) #画刻度
plt.xlim(0,120)
plt.grid(axis='x',linestyle='-.') #画竖线
#plt.text(100,80,'atm',ha = 'center',va = 'bottom',fontsize=7)#加标签
#ax.set_yticks([])#隐藏y轴刻度
plt.yticks(fontproperties = 'Times New Roman', size = 23)
plt.xticks(fontproperties = 'Times New Roman', size = 23)
plt.show() #展示
def fitc(name):
#提取数据
x = df['w']
layer = df[name]
x = x.values
layer = layer.values
print()
print("正在拟合"+name+"曲线")
print("共使用4个拟合峰,参数如下:")
#打开画布
plt.figure(1)
plot_scatter(x,layer)
# 设置范围
# v = [y0, amp, pos, fwhm]
# g = [y0,A,xc,w]
# "偏置","幅值","中心位置","宽度"
v1 = [500, 100, 10, 0]
v3 = [7000, 2000, 60, 100]
v2 =[500, 100, 50, 0]
v4 = [7000, 2000, 90, 100]
g1 = [200,5000,0,0]
g3 = [7000,9999000,1,100]
g2 = [100,0,-50,0]
g4 = [7000,2000,200,500]
popt,pcov = curve_fit(my_fit_cure,x,layer,\
bounds =([v1[0],v1[1],v1[2],v1[3],v2[0],v2[1],v2[2],v2[3],g1[0],g1[1],g1[2],g1[3],g2[0],g2[1],g2[2],g2[3]],\
[v3[0],v3[1],v3[2],v3[3],v4[0],v4[1],v4[2],v4[3],g3[0],g3[1],g3[2],g3[3],g4[0],g4[1],g4[2],g4[3]]))
plot_nihe(x,popt,'my_fit_cure')
#保存数据
#save_name = name + '.npy'
#np.save(save_name,popt)
#data = np.load('a.npy')
ready_to_show()
if __name__=='__main__':
df = pd.read_csv('筛选后的数据.csv')
name = '2L'
fitc(name)
1 | output: |